Question 1091209: Find the volume of the pyramid enclosed in the first octant by the origin and the intercepts of the plane x + 2y + z = 6.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The base of this pyramid at the plane y = 0 is an isosceles right-angled triangle with the legs of the length of 6 units.
So, its area is 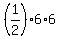 = 18 square units.
The height of this pyramid is y-intercept and, therefore, has the length of 3 units.
Therefore, the volume of the pyramid is = 18 square units.
The height of this pyramid is y-intercept and, therefore, has the length of 3 units.
Therefore, the volume of the pyramid is 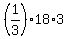 = 18 cubic units. = 18 cubic units.
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The formula for the volume of a pyramid is

where B is the area of the base an h is the height.
In this problem, we can choose the base to be the face of the pyramid in the xy plane, the face in the xz plane, or the face in the yz plane. If you want practice in working this kind of problem, you might want to work the problem all three ways and see that you get the same answer.
The intercepts of the given plane are (6,0,0), (0,3,0), and (0,0,6). Suppose we use the face in the xy plane (z=0) for our base. Then the base is the right triangle formed by the origin and the x and y intercepts; (0,0,0), (6,0,0), and (0,3,0). The legs of that right triangle are 6 and 3, so the area of that base is

and the height is the distance from the origin to the z-intercept, which is 6. So the volume of the pyramid is

Again, if you want to get practice in visualizing the pyramid and finding its volume by this method, you can go through the above calculations again using the face in the xz plane or yz plane as the base.
|
|
|