Question 10910: One angle of a triangle is 2 degrees larger than another angle. The sum of these two angles is 28 degrees larger than the third angle. How large are the three angles?
x+2+x=y+28?
2x+2=y+28?
then what??? (assuming this is the right set up)
Answer by kinupanda(9)   (Show Source):
You can put this solution on YOUR website! We have three angles: one angle is two degrees larger than another. Let's define the smaller of these two angles as  . Thus, we can define the larger angle in terms of , as  .
We can also define the third angle in terms of the other two! The problem tells us that the sum of the first two angles, e.g., 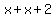 , is 28 degrees larger than the third. Rewording this, we know that the third angle is 28 degrees *smaller* than the sum of the other two. Thus, the measure of the third angle is equal to  =  .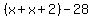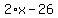
So now we have three expressions for the angles of this triangle: , , and 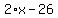 . But how do we solve for ?
Remember, in any triangle, the sum of the measures of the angles is always 180 degrees. Thus:  .
Simplifying this yields:
Now, we substitute x into the expressions we calculated earlier. Thus, the measure of the first angle is equal to degrees, the second is  degrees, and the third is  degrees.
Thus, our triangle's angles are 51, 53, and 76 degrees. To verify that this solution is correct, we just need to add them up. Sure enough,  , which we know should be the sum of the angles of a triangle.
|
|
|
