Question 1087752: A farmer is fencing off space for his chickens using two rolls of wire fence that are equal in length. One entire roll of wire fence is used to enclose space A in the shape of a regular polygon with 8 sides, and the entire second roll is used to enclose space B in the shape of a regular polygon with 5 sides. If each side of B is 6 feet longer than each side of A, what is the length, in feet, of one roll of wire fence?
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
One line short solution is
8x = 5*(x+6) ====> 8x = 5x + 30 ====> 3x = 30 ====> x = 10 ft
is the length of one side of the 8-sided polygon, so the entire perimeter of each polygon is 8*10 = 80 ft.
Answer. The length of each roll of wire fence is 80 ft.
Solved.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! Start by defining a variable:
 = length (in feet) of each side of the regular polygon with 8 sides (space A).
Now, you know that the length (in feet) of the roll used to fence space A is
 ,
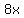which is what you want to find.
You also know that
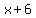 = length (in feet) of each side of the regular polygon with 5 sides (space B),
and as a consequence, you can calculate the length (in feet) of the roll used to fence space B as
 .
Because the two rolls were "two rolls of wire fence that are equal in length",
the equation to write and solve is
 .
You solve that to find , and then use it to find .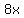
The length, in feet, of one roll of wire fence is  .
ANOTHER WAY:
Rolls of wire fence probably come in lengths that are integer numbers of feet,
and farmers like integers, so the lengths of the sides (in feet) of fenced spaces are probably whole numbers, like 1, 3, 5, 10.
Then the length (in feet) of a roll of wire fence must be a multiple of 8, and a multiple of 5.
The smallest one is  , and the others are multiples such as
 ,  ,  , and so on.
If the length of a toll were  feet,
the lengths (in feet) of the polygons' sides would be
 for space A, and
 for space B,
but 8 is not 6 more that 5,
so a 40 ft roll length does not make the side of space B 6 feet longer than the side of space A.
What about a length of  feet for the roll?
That would make the lengths (in feet) of the polygons' sides
 for space A, and
 for space B,
and  is  more that  ,
so an  -foot roll length is the solution.
It does make the side of space B exactly 6 feet longer than the side of space A.
|
|
|
