Question 1065525: What is the circumcenter of a triangle with a vertices of (2,4), (6,4), (2, 6)?
Found 2 solutions by Fombitz, ikleyn:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the midpoints of the sides,
A(2,4)
B(2,6)
C(6,4)
.
.
To find the midpoint, take the averages of the x and y values,
Midpoint of AC: (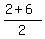 , ,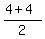 )=(4,4) )=(4,4)
Midpoint of AB: ( , , )=(2,5) )=(2,5)
Midpoint of BC: (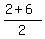 , , )=(4,5) )=(4,5)
.
.
Now find the lines through mAC and B(line 1), mAB and C(line 2), and mBC and A(line 3).
First find the slope, then use the point slope form of a line,
I'll use the designation 1, 2, 3 for the lines as defined in the previous sentence.
Line 1:




Line 2:





Now that we have two lines, we can calculate their intersection (which is the circumcenter),




and



.
.
.
 . .
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This triangle is RIGHT-ANGLED.
The circumcenter of ANY right-angled triangle lies in the midpoint of its hypotenuse.
The hypotenuse has vertices (6,4) and (2,6).
Its midpoint is x = (6+2)/2 = 8/2 = 4 and y = (4+6)/2 = 10/2 = 5.
Answer. The circumcenter is the point with the coordinates (x,y) = (4,5).
SOLVED.
For the fact that a circumcenter of a right-angled triangle is the midpoint of its hypotenuse, see the lesson
- Median drawn to the hypotenuse of a right triangle
in this site.
If you have questions or want to say "thanks", then please mention the ID number of this problem (# 1065525) in your response.
|
|
|