SOLUTION: im thinking of getting a tutor...however right now im really stuck on this question.Please help a.s.a.p A triangle has verticies A(0,4) B (-2,-2) C (6,2). Find the Centroid alg

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: im thinking of getting a tutor...however right now im really stuck on this question.Please help a.s.a.p A triangle has verticies A(0,4) B (-2,-2) C (6,2). Find the Centroid alg      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 105898: im thinking of getting a tutor...however right now im really stuck on this question.Please help a.s.a.p
A triangle has verticies A(0,4) B (-2,-2) C (6,2).
Find the Centroid algebraically
thanks sooooooooooooooo much to who ever helps me.. I'm brutal with math ;)
Answer by HyperBrain(694) About Me  (Show Source):
You can put this solution on YOUR website!
The centroid of a triangle is located at the intersection of the medians. A median is a line that originate from a corner of a triangle bisecting the opposite side.

Since you gave three points, it is a triangle and three unknown lines pass through these points.
First, let's find the line passing through A(0,4), and B (-2,-2).

slope=%28y-increment%29%2F%28x-increment%29
Let m=slope

m=%28-2-4%29%2F%28-2-0%29
m=%28-6%29%2F%28-2%29
m=3
Now, let's find the slope-intercept form.
y=mx%2Bb b is the y-intercept.
Let's use A (0,4) for x=0 and y=4.
4=0%2A3%2Bb
b=4
Thus the equation of line1 is y=3x%2B4
Now, let's find the equation of the line passing through B (-2,-2) andf C (6,2).
m=%282-%28-2%29%29%2F%286-%28-2%29%29
m=4%2F8
m=1%2F2
Let's use B(-2,-2)
y=mx%2Bb
-2=%28-2%29%2F%282%29%2Bb
-2=-1%2Bb
b=-1
Thus the equation of the line is
y=x%2F2-1

let's find the equation of the line passing through A(0,4) and C(6,2)
m=%282-4%29%2F%286-0%29
m=-2%2F6
m=-1%2F3
Let'd use A (0,4)
y=mx%2Bb
4=0%2Am%2Bb
b=4
threfore, the equation of the line is
y=-x%2F3%2B4
If we graph this three lines,
graph%281000%2C1000%2C-20%2C20%2C-20%2C20%2C-x%2F3%2B4%2Cx%2F2-1%2C3x%2B4%29
They form the triangle



Now, we should find the equations of the 3 medians.

the 1st median passes through A(0,4) and the midpoint of B and C
Let D=the midpoint of B and C
x-coordinate+of+D=%28%28x-coordinate+of+B%29%2B%28x-coordinate+of+C%29%29%2F%282%29
x-coordinate+of+D=%28-2%2B6%29%2F%282%29
x-coordinate+of+D=4%2F2=2
y-coordinate+of+D=%28%28y-coordinate+of+B%29%2B%28y-coordinate+of+C%29%29%2F%282%29
y-coordinate+of+D=%28-2%2B2%29%2F%282%29=0%2F2=0
Thus,
D=(2,0)
Now let's calculate the equation of the 1st median.
m=%280-4%29%2F%282-0%29=-4%2F2=-2
y=mx%2Bb
Let's use A(0,4)
4=0%2A%28-2%29%2Bb=0%2Bb
b=4
Thus, the equation of the 1st median is
y=-2x%2B4
The 2nd median passes through B(-2,-2) and the midpoint of A and C.
Let E=the midpoint of A and C
x-coordinate+of+E=%28%28x-coordinate+of+A%29%2B%28x-coordinate+of+C%29%29%2F%282%29
x-coordinate+of+E=%280%2B6%29%2F%282%29=6%2F2=3
y-coordinate+of+E=%28%28y-coordinate+of+A%29%2B%28y-coordinate+of+C%29%29%2F%282%29
y-coordinate+of+E=%284%2B2%29%2F%282%29=6%2F2=3
Thus,
E=(3,3)
Calculate for the equation of the 2nd median.
m=%283-%28-2%29%29%2F%283-%28-2%29%29=5%2F5=1
y=mx%2Bb
Use E(3,3)
3=3%2A1%2Bb
3=3%2Bb
b=0
Thus, the equation of the second median is
y=x
The last median passes through C and the midpoint of A and B.
Let F=the midpoint of A and B
x-coordinate+of+F=%28%28x-coordinate+of+A%29%2B%28x-coordinate+of+B%29%29%2F%282%29
x-coordinate+of+F=%280%2B%28-2%29%29%2F%282%29=-2%2F2=-1
y-coordinate+of+F=%28%28y-coordinate+of+A%29%2B%28y-coordinate+of+B%29%29%2F%282%29
y-coordinate+of+F=%284%2B%28-2%29%29%2F%282%29=2%2F2=1
Thus,
F=(-1,1)
Solve for the equation of the last median.
m=%282-1%29%2F%286-%28-1%29%29=1%2F7
y=mx%2Bb
Use F(-1,1)
1=-%281%2F7%29%2Bb
b=8%2F7
Thus, the equation is
y=x%2F7%2B8%2F7
Locating the centroid,

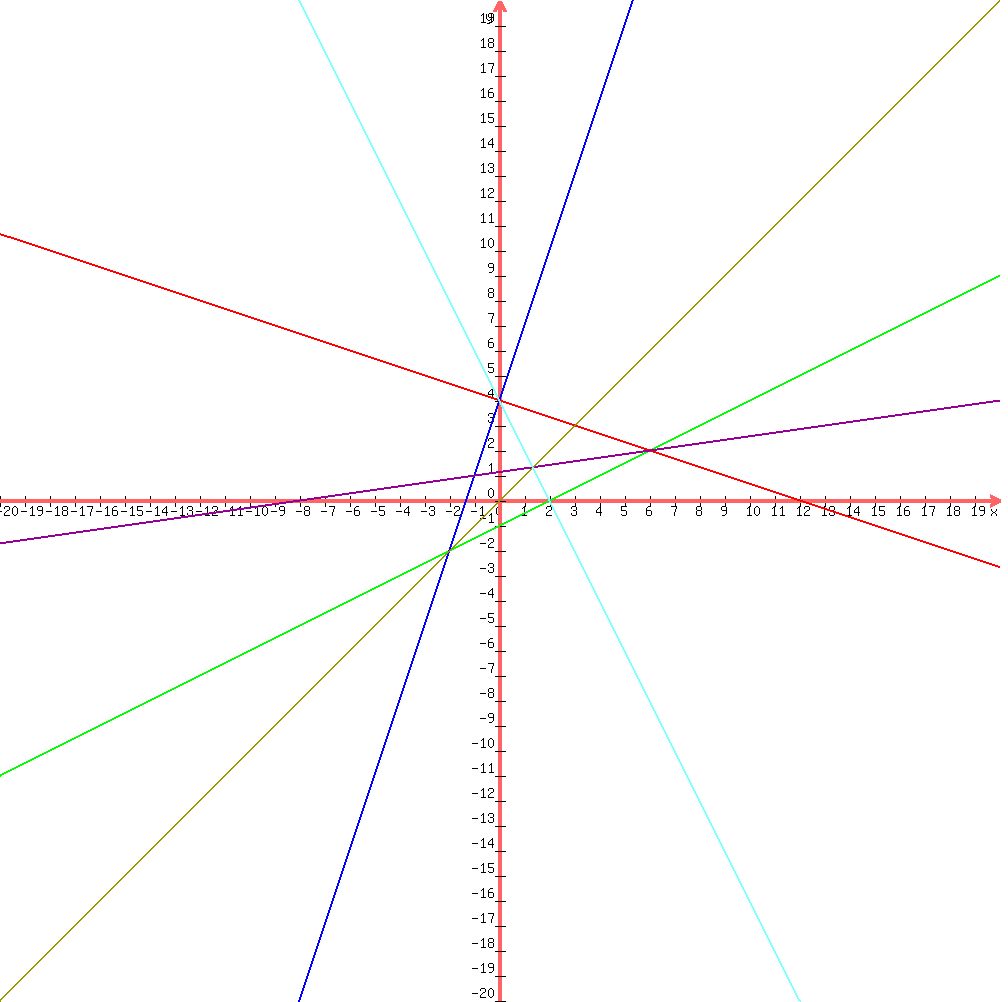
It is located at (4%2F3,4%2F3)

Boy, that's challenging can I have my prize?

Power up,
HyperBrain!