SOLUTION: The area of a rectangular field is 2c³-c²+6 square units. If the length of the field is c−2 units, what is its width?

First let's do this simpler one:

A = LW

Substitute 5 for A and 3 for L:

5 = 3W

Divide both sides by 3





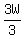
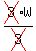  1
3)5
  3
  2
Answer: The width is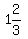  

Now let's do yours exactly the same way:

A = LW

Substitute 2c³-c²+6 for A and c-2 for L:

2c³-c²+6 = (c-2)W

Divide both sides by (c-2)





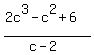
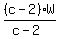
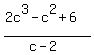
         2c² + 3c + 6
c-2)2c³ - c² + 0c + 6
    2c³ -4c²
         3c² + 0c
         3c² - 6c
               6c + 6
               6c -12
                   18
  

Answer: The width is  

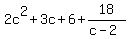Edwin