SOLUTION: In triangle ABC, point X is the midpoint of line AC and Y is the point one-third of the way from B to C. Segments AY and BX intersect at point Z. Find the ratio AZ : ZY.

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: In triangle ABC, point X is the midpoint of line AC and Y is the point one-third of the way from B to C. Segments AY and BX intersect at point Z. Find the ratio AZ : ZY.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1029869: In triangle ABC, point X is the midpoint of line AC and Y is the point one-third of the way from B to C. Segments AY and BX intersect at point Z. Find the ratio AZ : ZY.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Without loss of generality, situate triangle ABC on the Cartesian coordinate plane, with A(0,0), B(b,c), and C(a,0). (The triangle has base on the positive x-axis.
With these points, it could be determined that X(a/2, 0) and Y(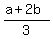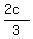%28a%2B2b%29%2F3, %282c%29%2F3).
Now the line BX will have equation y+=+%28c%2F%28b-a%2F2%29%29%28x-a%2F2%29, or y+=+%28%282c%29%2F%282b-a%29%29%28x-a%2F2%29.
On the other hand, line AY will have equation y+=+%28%282c%29%2F%28a%2B2b%29%29x.
The intersection of lines BX and AY is point Z, which after solving is found out to be (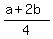%28a%2B2b%29%2F4, c%2F2).
From here it becomes easy: .
The preceding calculation was based on ratios as determined from the x-coordinates. A similar calculation based on ratios from the y-coordinates still yield the same value of 3.