SOLUTION: the legs of a right triangle are in the ratio 3:4 and its area is 1014 cm^2. find the length and perimeter

It is 3:4:5 right-angled triangle.
   (If in a right-angled triangle the two legs are in the ratio 3:4, then the hypotenuse is 5 units long. 
    Everybody knows it).

So, the length of one leg is 3 units, the length of the second leg is 4 units, and the length of the hypotenuse is 5 units.

Then the area of the triangle is half the product of its legs measures, i.e.  = , 
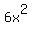where x is the length of that unit.

From the condition, you know that the area is 1014 .

It gives you an equation

 = .

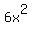Hence,   =  = 169   and   x = 13 cm.

Now one leg is 3*13 = 39 cm,  the other leg is  4*13 = 52 cm,  and the hypotenuse is  5*13 = 65 cm.

Thus the perimeter = 39 + 52 + 65 = 156 cm