Question 1019740: The height of a triangle is 4 in. greater than twice its base. The area of the triangle is no more than 168 in.2. Which inequality can be used to find the possible lengths, x, of the base of the triangle?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the area of a triangle is equal to 1/2 * base * height.
let a = area and b = base and h = height and the formula becomes a = 1/2 * b * h
you are given that the height is equal to 4 inches greater than twice the base.
since h = height and b = base, the formula for that would be h = 2b + 4
in the formula of a = 1/2 * b * h, replace h with 2b + 4 to get:
a = 1/2 * b * (2b + 4)
simplify to get a = 1/2 * 2b^2 + 4b
simplify further to get a = b^2 + 2b
since you want the area to be no more than 168 square inches, then you get a <= 168.
since a = b^2 + 2b, then you get b^2 + 2b <= 168 after you replaced a with it's equivalent value of b^2 + 2b.
so the formula you want is b^2 + 2b <= 168.
if you subtract 168 from both sides of that equation, you will get b^2 + 2b - 168 <= 0
to find the zero crossing points, set b^2 + 2b - 168 = 0.
you will find that the roots of that equation are b = -14 or b = 12.
you have 3 intervals on your graph you need to examine.
they are:
b < -14
b >= -14 and b <= 12
b > 12
you will find that the graph is less than or equal to 0 in the interval where b >= -14 and b <= 12
the graph looks like this:
on the graph, the variable x is used in place of b.
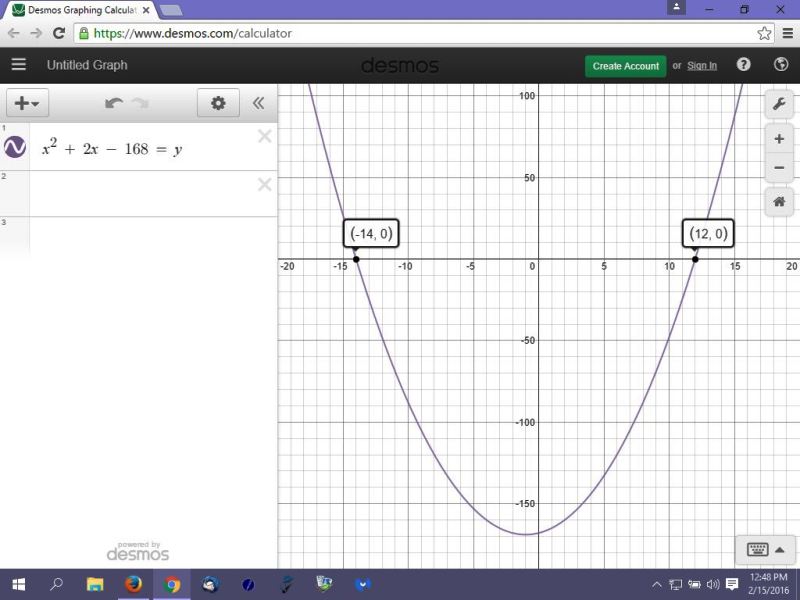
since the length of the base can't be less than or equal to 0, than you have that 0 < b <= 12.
when b = 12, h = 24+4 = 28, and a = 1/2 * b * h = 1/2 * 12 * 28 = 168.
when b = 11, h = 22+4 = 26, and a = 1/2 * b * h = 1/2 * 11 * 26 = 143.
when b = 0, the triangle collapses into a straight line.
it's debatable you can still call it a triangle, but if you think about sin(90) = 1, that only occurs when the triangle has collapsed, so you might think yes, but i've seen other sources that say no.
i'm assuming no in this presentation which is why i say the base can't be 0.
|
|
|