SOLUTION: the medians of a right triangle that are drawn from the vertices of the acute angles have lengths of 2 square root 13 and square root 73. find the lengths of the hypotenuse.

Solution

We will use this property of a median, which is valid for any triangle:

  In a triangle with the sides a, b and c, the median drawn to the side c has the length  = .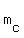

See the lesson The length of a median of a triangle in this site.

Next, let us apply the property to a right-angled triangle, whose legs are a and b units long and the hypotenuse is c units long.

For the medians    and    drawn to the legs a and b respectively, we will have

 = ,   = . 

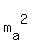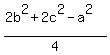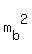Therefore,

 +  =  +  =  = .

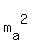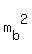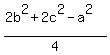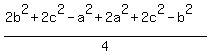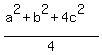Since for the right-angled triangle  = , you can rewrite the above equality in the form

 +  =  = .

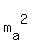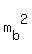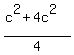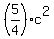Now substitute the given data   = 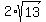  and   = 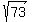. You will get

 =  = .

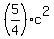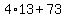It implies   =  = .

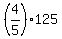Hence, c = 10.

The problem is solved.