Question 1011166: A regular polygon's interior angle is 8 times as large as its exterior angle
Found 3 solutions by jim_thompson5910, ikleyn, MathTherapy:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! E = exterior angle
I = interior angle
I = 8*E since the "interior angle is 8 times as large as its exterior angle"
Each pair of interior and exterior angles add up to 180 degrees
E + I = 180 degrees
E + 8*E = 180 ... replace I with 8E; solve for E
9E = 180
E = 180/9
E = 20
Each exterior angle is 20 degrees
Now let n = number of sides. We can tie n and E together with this formula
E = 360/n
Solve for n to get n = 360/E. Now plug in E = 20
n = 360/E
n = 360/20
n = 18
So there are 18 sides of this polygon.
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A regular polygon's interior angle is 8 times as large as its exterior angle
----------------------------------------------------------------------------
Hello,
your posting is not complete! A question is absent.
Therefore, I will add the question instead of you, as I understand it.
The question is: Find the number of sides of the polygon.
----------------------------------------------------------------------------
First let us find the interior angle  .
According to the condition, .
According to the condition,
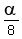 + +  = 180°.
Hence, = 180°.
Hence,  + + 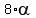 = 180°*8, or = 180°*8, or 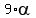 = 180°*8, or = 180°*8, or  = = 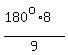 = 20°*8 = 160°.
Now find n, the number of sides, from the equation = 20°*8 = 160°.
Now find n, the number of sides, from the equation
 = 160, or
(n-2)*180 = n*160 -----> (n-2)*9 = n*8, -----> 9n - 18 = 8n -----> 9n - 8n = 18 -----> n = 18.
Answer. The number of sides of the regular polygon is 18. = 160, or
(n-2)*180 = n*160 -----> (n-2)*9 = n*8, -----> 9n - 18 = 8n -----> 9n - 8n = 18 -----> n = 18.
Answer. The number of sides of the regular polygon is 18.
Answer by MathTherapy(10559)   (Show Source): (Show Source):
|
|
|