This Lesson (Find the side of a square if distances are given from an interior point to 3 its vertices) was created by by ikleyn(52785)   : View Source, ShowAbout ikleyn:
Find the side of a square if distances are given from an interior point to 3 its vertices
Problem 1From the point inside a square, the distance to three corners are 4, 5 and 6 m, respectively.
Find the length of the side of a square.
Solution
Let ABCD be the square with the side of the length "a" in a coordinate plane,
A = (0,0), B = (a,0), C = (a,a) and D = (0,a).
Let (x,y) be the point inside the square ABCD with the distance 4 from A, 5 from D and 6 from B.
Thus we have these three equations ("distances")
x^2 + y^2 = 4^2, (1)
(a-x)^2 + y^2 = 6^2, (2)
x^2 + (y-a)^2 = 5^2. (3)
Making FOIL in equations (2) and (3), I can re-write them in this form
x^2 + y^2 = 16, (4) (= same as (1) )
a^2 - 2ax + x^2 + y^2 = 36, (5)
x^2 + y^2 - 2ay + a^2 = 25. (6)
Replacing x^2 + y^2 by 16 in equations (5) and (6), I obtain new equations instead of them
a^2 - 2ax = 20 (7)
a^2 - 2ay = 9 (8)
From equations (7) and (8), x = 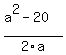 , y = , y = 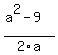 .
Substituting these expressions for x and y into equation (4), you get .
Substituting these expressions for x and y into equation (4), you get
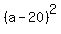 + + 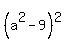 = = 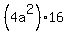 ,
or, simplifying ,
or, simplifying
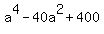 + + 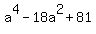 = = 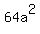 , ,
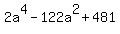 = 0.
From this bi-quadratic equation, you get for = 0.
From this bi-quadratic equation, you get for  , by applying the quadratic formula , by applying the quadratic formula
 = = 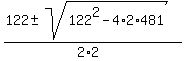 = = 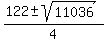 .
The smaller value does not work for "a" (it is easy to check), leaving the larger value .
The smaller value does not work for "a" (it is easy to check), leaving the larger value
 = = 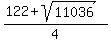 as the only meaningful solution.
Thus a =
as the only meaningful solution.
Thus a = 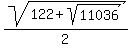 = 7.534 (approximately). = 7.534 (approximately).
My other lessons on Miscellaneous advanced Geometry problems in this site are
To navigate over all topics/lessons of the Online Geometry Textbook use this file/link GEOMETRY - YOUR ONLINE TEXTBOOK.
This lesson has been accessed 2266 times.
|