Lesson Find a triangle with integer side lengths and integer area

Find a triangle with integer side lengths and integer area

Problem 1

Use the Heron's formula for the area of the triangle

    area = .


Here s = 54/2 = 27 is the semi-perimeter, a = 17, b and c are two other sides.

Since the perimeter is 54 and side "a" is 17, we have  b + c = 54 - a = 54 - 17 = 37.

Let "b" be the longest side of the triangle.

Then  b >= 37/2 = 18.5  and since b is integer, we can write  b >= 19.

Also,  b is less than semi-perimeter b < 54/2 = 27;  c = 37-b.


Then the formula takes the form

    area =  = .   (*)


So, we seek for the integer value of "b" in the interval  19 <= b <= 26, which makes 
the right side of expression  (*)  integer number.


   +----------------------------------------------------------+
   |   Then one of the factors (27-b) or (b-10) should be 5,  |
   |                which gives  b = 25.                      |
   +----------------------------------------------------------+


Indeed, then b = 25 is the sought side length, and the area (*) is

    area = 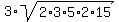 =  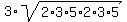=  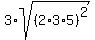= 3*2*3*5 = 90 square units.



    Thus the triangle sides are  a= 17,  b= 25  and  c= 37-25 = 12 units; 

                       the longest side is 25 units.

    The triangle inequalities are held, so such triangle does exist.

                 All requirements of the problem are held.



ANSWER.  Such a triangle does exist, and its longest side is 25 units long.

         This solution is a unique :  there is no other solution.