Question 985541: I need to find a formula to answer an investment increase word problem. I know the interest rate compounded annually and the total amount received. I need to find the original investment amount.
Found 3 solutions by macston, stanbon, solver91311:
Answer by macston(5194)   (Show Source):
You can put this solution on YOUR website! P=principal (original investment); r=interest rate (expressed as decimal); t=time(must match rate time- if rate is 5% per year, time must be in years); I=amount of interest.
.
I=Prt Can be solved for any of the variables.
P=I/rt Divide each side by rt.
r=I/Pt Divide each side by Pt.
t=I/Pr Divide each side by Pr.
.
To find original investment, P, you must know (or be able to calculate) Interest received (I), interest rate (r), and time invested (t).
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! I need to find a formula to answer an investment increase word problem. I know the interest rate compounded annually and the total amount received. I need to find the original investment amount.
----------
General Formula:: A(t)=P(1+(r/n))^(nt)
------------------------
Your Problem::
Solve for "P"
P = (A(t))/(1+(r/n))^(nt)
------------------------------
Cheers,
Stan H.
----------------
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website!
The pieces of a compound interest problem are the future value,  , the present value,  , the interest rate expressed as a decimal,  , the number of compounding periods per year,  , and the number of years, 
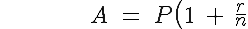^^{nt})
^^{nt}})
}{n\ln\left(1\ +\ \frac{r}{n}\right)})
}{nt}}\ -\ 1\right\])
John
My calculator said it, I believe it, that settles it
|
|
|
