Question 924680: A local cinema found that if the price of admission was $13, the attendance was about 750 customers per day. When the price of admission was dropped to $12, attendance increased to about 1900 per day. Write a linear equation for the attendance in terms of the price, p. ( A = mp + b )
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A local cinema found that if the price of admission was $13, the attendance was about 750 customers per day. When the price of admission was dropped to $12, attendance increased to about 1900 per day. Write a linear equation for the attendance in terms of the price, p. ( A = mp + b )
Let price be x, and attendance, y
Attendance: 750 customers, when PRICE = $13
Attendance: 1,900 customers, when PRICE = $12
We then get the points, (13, 750) & (12, 1,900)
Slope of linear equation, or m =  , or , or 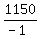 , or - 1,150 , or - 1,150
Using coordinate point (13, 750), and slope (m) = - 1,150, the point-slope form:
 becomes: becomes:
y – 750 = - 1,150(x – 13)
y – 750 = - 1,150x + 14,950
y = - 1,150x + 14,950 + 750
y = - 1,150x + 15,700, or 
|
|
|