|
Question 825088: (1) The total cost of 12kg of apples and 24kg of oranges is #2160, and the total cost of 24kg of apples and 12kg of oranges is #1800. Find the total cost of 3kg of apple and 10kg of oranges.
(2) A man's income from interest is #500. He doubles his investment and also gets an increase of 5% in wages And his Income increases to #800. What was his original income separating in terms of interest(I) and wages(W)
(3) A student scores 5x marks In the first exam papers and x+10 marks in the second. He came second in the exam. The first student scoring a total of 118 marks. Find the range of value of x.
Answer by josgarithmetic(39632)   (Show Source): (Show Source):
You can put this solution on YOUR website! The q#1 is a simple two-variable system of equation exercise. The #2 and #3? Maybe not.
#1:
We want variables for price of oranges and price of apples. Pounds(money unit) per kilogram.
x = apple price
y = orange price
 and and 
'
 and and 
 , and , and  so subtract the second equation from the first equation. so subtract the second equation from the first equation.
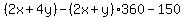

 , pounds per kilogram oranges. , pounds per kilogram oranges.
 , pounds per kilogram apples. , pounds per kilogram apples.
'
Use these x and y to answer your question.
#3:
You are not clear about, "student" and "first student". You might mean, a student scored 5x and x+10. The only student who scored better received 118 for marks. This must mean that the 118 marks is greater than the 5x+x+10 marks.
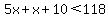 , and naturally, , and naturally,  ; ;
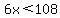 , and , and  ; ;
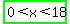
As a practical feel, I'd imagine x must really be 1 or more, so a better choice about x is to say:
 ; but that choice may be just arbitrary. ; but that choice may be just arbitrary.
|
|
|
| |