Question 769332: The formula for determining interest compounded monthly is A = P(1 +(r/12))12t, where A represents the amount invested after t years, P the principal invested, and r the interest rate. Jimmy invests $1,000 at an interest rate of 10% for 3 years, while Jenny invests $1,000 at an interest rate of 5% for 6 years.
Part 1: Determine the amount of return gained by Jimmy and Jenny.
Part 2: Summarize your results from Part 1, including how you arrived at your answer.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! It's just a question of applying the formula

In that formula,  is the rate expressed as a decimal, is the rate expressed as a decimal,
so it is  for 10% interest and for 10% interest and  for 5% interest. for 5% interest.
Jimmy ends up with
$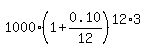 =$ =$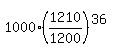 =$ =$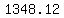
He gained $ , which is 34.8% of the amount he invested. , which is 34.8% of the amount he invested.
Jenny ends up with
$ =$ =$ =$ =$
She gained $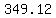 , which is 34.9% of the amount she invested. , which is 34.9% of the amount she invested.
Percentages are ratios amd can be used as factors.
10% means 10 for each 100, or the ratio 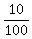
That ratio is a fraction, and can be written as a decimal.

10% interest means $10 interest for $100 deposit, or 10 cents for each 100 cents ($0.10 for $1.00).
So for simple 10% interest for 1 year, to could multiply times 
For 5% simple interest for a year you would multiply times  . .
For 10.25%, you would multiply times 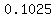 . .
For 3.75%, you would multiply times 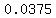 . .
And so on.
|
|
|