Question 693463: The percent increase for an in-state tuition at a certain public university during the years 1991 through 1999 can be modeled by the quadratic function defended by f(x)= 0.156x2( power) -2.02x+10.2, where x=1 represents 1991, x=2 represents 1992, and so on.
* based on this model, by what percent ( to the nearest tenth) did the tuition increase in 1993?
* in what year was the minimum tuition increase? ( round to the nearest year.) to the nearest tenth, by what percent did tuition increase that year?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The percent increase for an in-state tuition at a certain public university during the years 1991 through 1999 can be modeled by the quadratic function defended by f(x)= 0.156x2( power) -2.02x+10.2, where x=1 represents 1991, x=2 represents 1992, and so on.
:
f(x)= 0.156x^2 - 2.02x + 10.2,
:
* based on this model, by what percent ( to the nearest tenth) did the tuition increase in 1993?
x = 3
f(x) = 0.156x^2 - 2.02x + 10.2
f(3) = .156(3^2) - 2.02(3) + 10.2
f(3) = 1.404 - 6.06 + 10.2
f(3) = 5.5%
:
* in what year was the minimum tuition increase? ( round to the nearest year.) to the nearest tenth, by what percent did tuition increase that year?
:
The minimum occurs at the axis of symmetry. x = -b/(2a)
x = 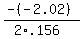
x = 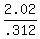
x = 6.474 ~ 6 which is 2006
:
Find the percent when x = 6
f(6) = 0.156(6^2) - 2.02(6) + 10.2,
f(6) = 5.6 - 12.12 + 10.2
f(6) ~ 3.7% increase in 2006, the minimum
|
|
|