SOLUTION: The balance on joe's credit card is 8000. payments are made monthly but interest is compounded daily. The stated APR is 18. Joe has since cut up the credit card and wishes to pay o

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: The balance on joe's credit card is 8000. payments are made monthly but interest is compounded daily. The stated APR is 18. Joe has since cut up the credit card and wishes to pay o      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 662277: The balance on joe's credit card is 8000. payments are made monthly but interest is compounded daily. The stated APR is 18. Joe has since cut up the credit card and wishes to pay off the balance in 5 years. What should his monthly payment be to reach his goal?
(1+.18/365)^(365/12)-1 =1.015% this is the correct rate but I am not sure how to find the actual amount joe will need to pay monthly to answer this question.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
DISCLAIMER: I am not into finance. I am just a math/science-loving old chemist.

I agree that to calculate the interest accrued over 1 day, you would multiply times 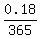0.18%2F365,
and that to calculate the balance after 1 day, you would multiply times 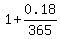1%2B0.18%2F365,
and that to calculate the balance after 1 month, you would multiply times 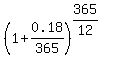%281%2B0.18%2F365%29%5E%28365%2F12%29.
%281%2B0.18%2F365%29%5E%28365%2F12%29=1.01511 (conveniently rounded) as per my computer.
The monthly interest rate would be 0.01511 (as a decimal), or 1.511% per month.

On my computer, using Excel, the function
PMT(0,01511,60,8000)=$203.72
calculates the monthly payment needed to pay off
$8000, in 60 months, at an interest of 1.511%,
making payments at the end of each month.

Bank people probably have even easier ways to calculate it,
but I like to understand the algebra in it,
and here is what I understand:
One month after starting the loan,
with the interest accrued, the balance would be
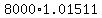$8000%2A1.01511, but at that point Joe pays $x,
and the new balance is $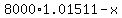8000%2A1.01511-x
A month later, the same thing happens, and the balance becomes
$%288000%2A1.01511-x%29%2A1.0511-x=8000%2A1.01511%5E2-1.01511%2Ax-x
Calling 1.01511=R to save ink,
the balance is $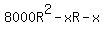8000R%5E2-xR-x after 2 months,
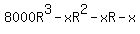$8000R%5E3-xR%5E2-xR-x after 3 months,
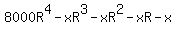$8000R%5E4-xR%5E3-xR%5E2-xR-x after 4 months, and so on.
After 5 years (60 months), the balance is
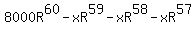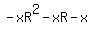$8000R%5E60-xR%5E59-xR%5E58-xR%5E57.........-xR%5E2-xR-x=$0
So, 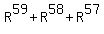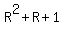8000R%5E60=x(R%5E59%2BR%5E58%2BR%5E57.........%2BR%5E2%2BR%2B1%29)
It is not hard to prove that the sum in brackets can be calculated as
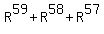R%5E59%2BR%5E58%2BR%5E57.........%2BR%5E2%2BR%2B1=%28R%5E60-1%29%2F%28R-1%29
So we can write the equation above, using the simpler sum calculation, as
8000R%5E60=x%28R%5E60-1%29%2F%28R-1%29
And now we can solve for x
8000R%5E60=x%28R%5E60-1%29%2F%28R-1%29 --> x=8000R%5E60%28R-1%29%2F%28R%5E60-1%29
The computer calculated for me
R%5E60=1.01511%5E60=2.45906 (conveniently rounded),
R%5E60-1=1.01511%5E60-1=2.45906-1=1.45906 (conveniently rounded),
and we know R-1=1.01511=0.01511
So the good enough approximation is x=8000%2A2.45906%2A0.1511%2F1.45906=203.73
(Using R=0.015 yields x=203.15, which is less accurate).