Question 644020: After a student wrote a $1,400 check to pay for a car, he had a new balance of $700 in his account. What was the account balance before he wrote the check?
$2,100 is the amount but on my online home work it has this:
x − 1,400 + what = 700 + 1,400
I put 700 but they said I was wrong
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The expected answer is  . .
That is what you have to add to both sides of the equal sign as a first step to solve the  equation you would start with (calling the initial balance that you have to find equation you would start with (calling the initial balance that you have to find  ). ).
 --> -->  --> --> 
The computer grading your homework may accept only "1400", only "1,400" or both.
(My son went through an online school, so I know the format of your answer often matters).
What they are trying to do is train you to solve equations by following a fixed procedure.
With some luck, you will understand the situations described and see the logical way to solve problems, rather than blindly following a procedure.
The procedure to solve an equation that has  on only one side of the equal sign works like this: on only one side of the equal sign works like this:
Step 1 - write an equation to describe the information you have.
You would write  to describe that starting with a balnce of to describe that starting with a balnce of  , ,
after spending (subtracting) 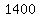 from that, you got from that, you got  left. left.
Step 2 - Undo what was done to that  step by step, and in reverse order, but to keep the equal sign valid you must do the same thing to both sides of the equal sign. step by step, and in reverse order, but to keep the equal sign valid you must do the same thing to both sides of the equal sign.
On the left hand side there is 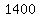 subtracted from subtracted from  . So you add . So you add 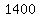 to both sides, because if that equal sign was valid, it will still be valid after adding the same number to both sides (and viceversa). to both sides, because if that equal sign was valid, it will still be valid after adding the same number to both sides (and viceversa).
If you had a more complicated equation, like  , you would reason that the , you would reason that the  would have been multiplied times would have been multiplied times  first, and that first, and that  was added after that. was added after that.
Your solution would look like this
 --> -->  (undoing the adding of (undoing the adding of  ) )
 --> -->  (simplifying and calculating as you can on both sides) (simplifying and calculating as you can on both sides)
 --> -->  (dividing by (dividing by  to undo the multiplication times to undo the multiplication times  ) )
 --> -->  (simplifying and calculating as you can on both sides). (simplifying and calculating as you can on both sides).
|
|
|