|
Question 579312: Suppose you have a cookie stand, and when you charge $3 per cookie box you sell 250 boxes. But when you raise your price to $5 you only sell 120 boxes.
a. Write an equation for the number of boxes you sell as a function of the price you charge.
b. Denote "B" for number of boxes, and "P" for the price you charge.
c. Assume the function is linear
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x equal the cost per cookie box.
let y equal the number of cookie boxes you sell.
you have 2 points that you can use to make a straight line equation.
they are:
(x1,y1) = (3,250)
(x2,y2) = (5,120)
these 2 points can be used to generate a straight line equation using the point slope form.
the point slope form of the equation for a straight line is:
y - y1 = m * (x - x1)
it can also be:
y - y2 = m * (x - x2)
any point that is on the line can be used.
m is the slope of the equation.
the formula to find the slope is:
m = (y2 - y1) / (x2 - x1)
you use both points to find the slope.
substituting for y1 and y2 and x1 and x2, we get:
m = (120 - 250) / (5 - 3)
this becomes:
m = -130 / 2 which becomes:
m = -65
our slope is -65 and our equation becomes:
y - y1 = -65 * (x - x1)
or it becomes:
y - y2 = -65 * (x - x2)
we can use either point.
we'll use (x1,y1) = (3,250)
when we use that point, our equation becomes:
y - 250 = -65 * (x - 3)
we simplify this to get:
y - 250 = -65x + 195
add 250 to both sides of this equation to get:
y = -65x + 195 + 250 which becomes:
y = -65x + 445
that's our equation.
the equation looks like this:
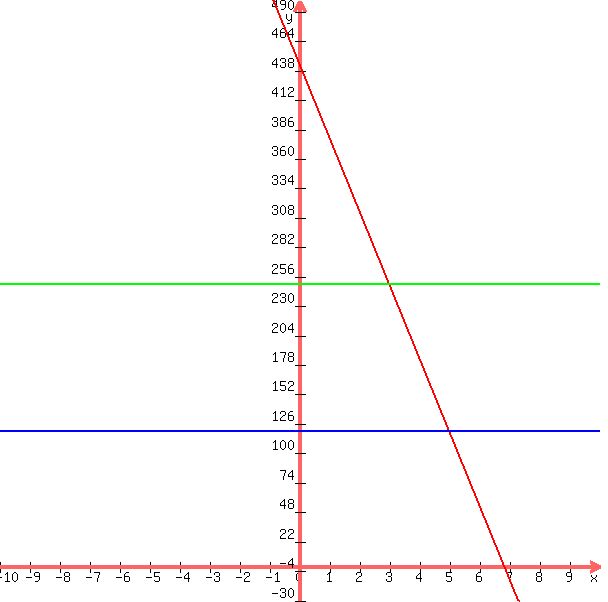
you can see from the graph that when x = 3, y = 250, and when x = 5, y = 120.
the horizontal lines at y = 250 and y = 120 are there to help you see that.
|
|
|
| |