Question 535620: In how may years is required for ₱ 2,000.00 to increase by ₱ 3,000 if interest is 12% compounded semi - annually?
Found 2 solutions by KMST, zuproc66:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! As I understand, no interest is added daily, but after half a year 6% interest is added. That would be
The total balance would then be
If the same thing happens in every half-year period, the balance is the same in between, but every six months interest is added, and the previous balance gets multiplied by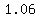 
That happens twice per year, or  times in  years.
If after years the balance is 3000 more
 -->
So, the 15th time interest is added, 7.5 years after deposit, the balance would have increased by 2793, to 4793. The next time interest is added will be 8 years after deposit, making the balance reach 5,080.70, increased by 3,080.70. You would need 8 years to reach the target balance, and then you would have exceeded it a bit.
If they kept adding interest to the balance daily (or even continuously), but only compounded semi-annually, then a 5000 balance would be reached at about 7.86 years, and you would not need to wait for the whole 8 years.
Answer by zuproc66(2)  (Show Source):
You can put this solution on YOUR website! compute first for the effective rate of interest:
eff i = (1 + (i/m))^m-1
where i = the interest which is 12% = 0.12
m = compounding period = semi annually = 2
eff i = (1 + (0.12/2)^2-1 = 0.1236
from the formula:
F = P(1+i)^n
where F = future worth, which is given at P5000 (3000+2000)
P = present worth which is given at P2,000
i = 0.1236 as solve above
n = number of years for the 2000 to increase by 3000 or become 5000
subs above values:
5000 = 2000(1+0.1236)^n
(1.1236)^n = 5000/2000
n = log (base 1.236) (5/2) = 7.8626 years or 8 years
|
|
|
