Question 514594: A man has 3 sums of money invested, one at 12%, one at 10% and the last at 8%, his total annual income from the three investments is 2100 the first investment yields as much as the other 2 combined, if he could receive 1% more on each investments his annual income would be increased by 202.50. How much is his investments at each rate?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A man has 3 sums of money invested, one at 12%, one at 10% and the last at 8%,
his total annual income from the three investments is 2100
the first investment yields as much as the other 2 combined, "
How much is his investments at each
:
Write an equation for each statement:
;
"A man has 3 sums of money invested, one at 12%, one at 10% and the last at 8%,
his total annual income from the three investments is 2100"
.12x + .10y + .08z = 2100
:
"the first investment yields as much as the other 2 combined, "
.12x = .10y + .08z
rewrite this to
.12x - .10y - .08z = 0
:
"if he could receive 1% more on each investments his annual income would be increased by 202.50"
.13x + .11y + .09z = 202.50 + 2100
.13x + .11y + .09z = 2302.50
:
Add these two equation
.12x + .10y + .08z = 2100
.12x - .10y - .08z = 0
------------------------addition eliminates y and z, find x
.24x = 2100
x = 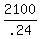
x = $8,750 invested at 12%
:
Find the return on this amt
.12(8750) = $1050
:
"the first investment yields as much as the other 2 combined, "
.10y + .08z = 1050
:
"receive 1% more on each investments his annual income would be increased by 202.50"
.01(8750) + .01y + .01z = 202.50
87.50 + .01y + .01z = 202.50
.01y + .01z = 202.50 - 87.50
.01y + .01z = 115
multiply by 10, subtract the previous equation
.10y + .10z = 1150
.10y + .08z = 1050
--------------------subtraction eliminates y, find z
.02z = 100
z = 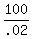
z = $5000 invested at 8%
:
Use equation: .01y + .01z = 115, to find y, replace z
.01y + .01(5000) = 115
.01y + 50 = 115
.01y = 115 - 50
.01y = 65
y = 
y = $6500 invested at 10%
:
Summarize:
x = $8750 invested at 12%
y = $6500 invested at 10%
z = $5000 invested at 8%
:
:
Check this by finding the total return using these values
.12(8750) + .10y(6500)+ .08(5000) =
1050 + 650 + 400 = 2100, confirms our solutions
|
|
|