Question 508192: Megs salary starts at 16,000 with annual raises of $1500. Janes salary starts at 19,300 with annual raises of 950. How many years will it be until they make the same amount. Set up in numeric form and solve
Found 2 solutions by stanbon, MathTherapy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Megs salary starts at 16,000 with annual raises of $1500. Janes salary starts at 19,300 with annual raises of 950. How many years will it be until they make the same amount. Set up in numeric form and solve
------
Meg(x) = 16000+1500x
-------
Jan(x) = 19300 + 950x
---
Solve:
16000+1500x = 19300 + 950x
---
13500x = 3300
----
x = 0.2444
===
Comment: Probably one or more of your posted numbers is wrong
----
Cheers,
Stan H.
==========
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! Megs salary starts at 16,000 with annual raises of $1500. Janes salary starts at 19,300 with annual raises of 950. How many years will it be until they make the same amount. Set up in numeric form and solve
Let years for the salaries to be the same be Y
Then Meg’s equation is: 16,000 + Y(1,500), and Jane’s: 19,300 + Y(950)
Setting them equal to each other gives us: 16,000 + Y(1,500) = 19,300 + Y(950)
16,000 + 1,500Y = 19,300 + 950Y
1,500Y – 950Y = 19,300 – 16,000
550Y = 3,300
Y, or years it’ll take for both to earn same salary = 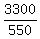 or or 
-------
Check
-------
In 6 years Meg will be making 16,000 + 6(1,500) or 16,000 + 9,000, or $25,000
In 6 years Jane will be making 19,300 + 6(950) or 19,300 + 5,700, or $25,000
As seen, both will be making the same annual salary in 6 year’s time.
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|