SOLUTION: In planning for a school dance, you find that one band will play for $250, plus 50% of the total ticket sales. Another band will play for a flat fee of $550. In order for the first

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: In planning for a school dance, you find that one band will play for $250, plus 50% of the total ticket sales. Another band will play for a flat fee of $550. In order for the first      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 221208: In planning for a school dance, you find that one band will play for $250, plus 50% of the total ticket sales. Another band will play for a flat fee of $550. In order for the first band to produce more profit for the school than the other band, what is the highest price you can charge per ticket, assuming 300 people attend?
i tried setting it up something like .50(250-x)+250>550 x= the price of tickets
but I am not getting the correct answer.
Found 2 solutions by josmiceli, MathTherapy:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
Let t = price/ticket in dollars to charge
Let P = profit for school
Write 2 equations, 1 for each band
(1)P+=+300t+-+250+-+300t%2F2
(1)2P+=+600t+-+500+-+300t
(1)2P+=+300t+-+500
(1)P+=+150t+-+250
and
(2)P+=+300t+-+550
If the profits from the 2 bands were equal,
150t+-+250+=+300t+-+550
150t+=+300
t+=+2
If the ticket price were $1.99
(1)P+=+150%2A1.99+-+250
(1)P+=+298.50+-+250
(1)P+=+48.50
and
(2)P+=+300%2A1.99+-+550
(2)P+=+597+-+550
(2)P+=+47
1st band is more profitable
If the ticket price were $2.01
(1)P+=+150%2A2.01+-+250
(1)P+=+301.50+-+250
(1)P+=+51.50
and
(2)P+=+300%2A2.01+-+550
(2)P+=+603+-+550
(2)P+=+53
Band (2) becomes more profitable for the
school, when the ticket price goes over
$2.00, so the ticket price has to be
under $2.00 to make more profit from 1st band


Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Let price of ticket be P

Then proceeds from sale of 300 tickets = 300P

Since the 1st band wants $250, plus 50% of ticket sales, then the school would have to pay the 1st band 250 + .5(300P), or 250 + 150P, and the profit from using the 1st band = 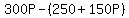300P+-+%28250+%2B+150P%29

Since the 2nd band wants a flat fee of $550, then the school would have to pay the 2nd band $550, and the profit from using the 2nd band = 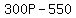300P+-+550

Since we're looking for the 1st band to make more profit for the school than the 2nd band, then we'll have:

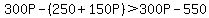
300P+-+%28250+%2B+150P%29+%3E+300P+-+550

300P - 250 - 150P > 300P - 550

300P - 150P - 300P > - 550 + 250

- 150P > - 300

P < 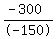%28-300%29%2F-150, or P < 2 ----- Take note that the inequality changes from > to < when dividing by a negative value

Therefore, in order for the 1st band to make more profit for the school than the 2nd band, the price of 300 tickets should be < $highlight_green%282%29 each.