SOLUTION: 2. A business invests $8,000 in a savings account for two years. At the beginning of the second year, an additional $2,500 is invested. At the end of the second year, the account

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: 2. A business invests $8,000 in a savings account for two years. At the beginning of the second year, an additional $2,500 is invested. At the end of the second year, the account      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 199561: 2. A business invests $8,000 in a savings account for two years. At the beginning of the second year, an additional $2,500 is invested. At the end of the second year, the account balance is $11,445. What was the annual interest rate?
Im not good at interest

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
A=P%281%2Br%29 Start with the interest formula. Note: since we're only concerned with year intervals, this means that t=1 (so we don't have to worry about exponents)


A=8000%281%2Br%29 Plug in P=8000 (since $8,000 is the original amount in the account)


A=8000%2B8000r Distribute


So after one full year, you now have 8000%2B8000r dollars in the account.



Now because "an additional $2,500 is invested", this pushes up the amount to 8000%2B8000r%2B2500 (just add 2500 to the last expression). Combine like terms to get 10500%2B8000r


So the new principal is P=10500%2B8000r


Since after two years you have $11,445, this means that A=11445


A=P%281%2Br%29 Go back to the original formula


11445=%2810500%2B8000r%29%281%2Br%29 Plug in A=11445, P=10500%2B8000r and r=1%2Br


11445=10500%2B18500%2Ar%2B8000%2Ar%5E2 FOIL


0=10500%2B18500%2Ar%2B8000%2Ar%5E2-11445 Subtract 11445 from both sides.


0=8000%2Ar%5E2%2B18500%2Ar-945 Combine like terms.


Notice we have a quadratic in the form of ar%5E2%2Bbr%2Bc where a=8000, b=18500, and c=-945


Let's use the quadratic formula to solve for r


r+=+%28-b+%2B-+sqrt%28+b%5E2-4ac+%29%29%2F%282a%29 Start with the quadratic formula


Plug in a=8000, b=18500, and c=-945


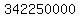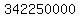r+=+%28-18500+%2B-+sqrt%28+342250000-4%288000%29%28-945%29+%29%29%2F%282%288000%29%29 Square 18500 to get 342250000.


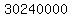r+=+%28-18500+%2B-+sqrt%28+342250000--30240000+%29%29%2F%282%288000%29%29 Multiply 4%288000%29%28-945%29 to get -30240000


r+=+%28-18500+%2B-+sqrt%28+342250000%2B30240000+%29%29%2F%282%288000%29%29 Rewrite sqrt%28342250000--30240000%29 as sqrt%28342250000%2B30240000%29


r+=+%28-18500+%2B-+sqrt%28+372490000+%29%29%2F%282%288000%29%29 Add 342250000 to 30240000 to get 372490000


r+=+%28-18500+%2B-+sqrt%28+372490000+%29%29%2F%2816000%29 Multiply 2 and 8000 to get 16000.


r+=+%28-18500+%2B-+19300%29%2F%2816000%29 Take the square root of 372490000 to get 19300.


r+=+%28-18500+%2B+19300%29%2F%2816000%29 or r+=+%28-18500+-+19300%29%2F%2816000%29 Break up the expression.


r+=+%28800%29%2F%2816000%29 or r+=++%28-37800%29%2F%2816000%29 Combine like terms.


r+=+0.05 or r+=+-2.3625 Divide


So the possible answers are r+=+0.05 or r+=+-2.3625


However, since you CANNOT have a negative interest rate, this means that the only possible answer is r+=+0.05


Now multiply by 100 to get 100%2A0.05=5.


=============================================

Answer:

So the annual interest rate is 5%