|
Question 165322This question is from textbook
: I ask this problem yesterday with no response.
A business invest $10,000 in a savings account for two years. At the beginning of the second year, an additional $3500 was invested. At the end of the second year, the account balance is $15,569.75. What is the interest rate?
This question is from textbook
Found 2 solutions by gonzo, Earlsdon:
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! today you get a response.
-----
10000 = investment at the beginning of year 1.
3500 = additional investment at the beginning of year 2.
-----
some assumptions:
investment is made at the beginning of each year.
interest is calculated at the end of each year.
the interest on the investment is compounded. this means that the principal remains in the account and the interest on the next year is the interest on the principal of the previous year plus the interest earned in that previous year.
-----
formula for interest on an investment that is compounded annually is:
f = p * (1+i)^n
where:
f is the future amount of the investment.
p is the present amount of the investment.
i is the annual interest rate
n is the number of years that interest has been applied.
-----
your original investment starts at the beginning of year 1 and interest is calculated to the end of year 2. that would be 2 years of interest (interest for year 1 and interest for year 2).
-----
the additional investment starts at the beginning of year 2 and interest is calculated to the end of year 2. that would be 1 year of interest (interest for year 2 only).
-----
the formula for the original investment is calculated as follows:
f1 = p1 * (1+i)^n1
where:
f1 = ?????
p1 = 10000
i = ????
n1 = 2
substituting for known values, this formula becomes:
f1 = 10000 * (1+i)^2
-----
the formula for the additional investment is calculated as follows:
f2 = p2 * (1+i)^n
f2 = ?????
p2 = 3500
i = ?????
n2 = 1
substituting for known values, this formula becomes:
f2 = 3500 * (1+i)^1
-----
let F = future value of both investments.
that means that F = f1 + f2
substitute for f1 and f2 in the equation and it becomes:
F = 10000 * (1+i)^2 + 3500 * (1+i)^1 (equation 1) *******************
-----
equation 1 will be used later on to prove the value of i that was found is correct.
-----
multiplying out all terms and the equation becomes:
F = 10000*1 + 10000*2*i + 10000*i^2 + 3500*1 + 3500*i
this becomes:
F = 10000 + 20000*i + 10000*i^2 + 3500 + 3500*i
combining like terms, and this equation becomes
F = 13500 + 23500*i + 10000*i^2
-----
this is the same as F = 10000*i^2 + 23500*i + 13500
-----
since we know the value of F, the equation becomes
15569.75 = 10000*i^2 + 23500*i + 13500
subtracting 15569.75 from both sides of the equation and it becomes:
0 = 10000*i^2 + 23500*i + 13500 - 15569.75
which becomes:
10000*i^2 + 23500*i -2069.75 = 0
-----
we can solve this using the quadratic formula:
quadratic formula is x =  or x = or x = 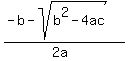 . .
it is used to solve quadratic equations in the form of  . .
our equation is in the same form, except we are substituting i for x.
-----
a = 10000
b = 23500
c = -2069.75
b^2 = 552250000
4ac = -82790000
sqrt (b^2-4ac) = sqrt (552250000 + 82790000) = sqrt (653040000) = 25200.
-b = -23500
2a = 20000
(-23500 + 25200) / 20000 = .085
(-23500 - 25200) / 20000 = -2.435
i is either .085 or -2.435.
unlikely it is -2.435 so we'll use .085.
-----
original equation for F is:
F = 10000 * (1+i)^2 + 3500 * (1+i)^1
assuming i = .085, then the equation for F becomes
F = 10000 * (1.085)^2 + 3500 * (1.085)^1
which becomes:
F = 10000 * 1.177225 + 3500 * 1.085
which becomes:
F = 11772.25 + 3797.5 which becomes:
F = 15569.75
-----
answer is i = .085.
-----
some comments:
this is not an easy problem.
if it were carried out more years with more investments along the way it would be enormously more difficult to solve.
it was solvable here because i was able to use the quadratic formula.
i'm not sure if i would have been able to solve it if there were another year of investment for more years making the quadratic formula not viable as a means of solution.
normally these problems are handled by computers doing multiple iterations to arrive at a solution.
good one.
thanks for the exercise.
-----
i thought there might be an easier way to solve it, but i couldn't find one.
-----
if the problem assumed simple interest, then it would have been easier to solve.
simple interest assumes interest on the initial investment only for all years.
in this problem, using simple interest, i would have calculated as follows:
interest on initial investment = 10000 * i * 2
interest on additional investment = 3500 * i * 1
principal plus interest = total
total = 15569.75
15569.75 = 10000 + 3500 + 20000*i + 3500*i
15569.75 = 13500 + 23500*i
15569.75-13500 = 23500*i
(15569.75-13500)/23500 = i
i = .088074468
-----
substituting in equation, we get
15569.75 = 13500 + 23500*.088074468
15569.75 = 13500 + 2069.75
15569.75 = 15569.75
-----
simple interest is much easier.
i suspect they wanted compound interest so the first solution is probably the one you are looking for with an interest rate of .085 per year, or 8.5% interest per year.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
|
|
|
| |