|
Question 128006: This is the third and final part of the questions I sent to you already.
3.You recently started the paperwork to purchase your new home, and youb were notified that you can move into the house in 2 weeks. You decide to hire a moving company, but are unsure which company to choose. You search online and are interested in contacting two companies, Heavy Lifters and Quick move, to discuss their rates. Heavy Lifting charges an $80 fee plus $35 per hour. Quick Move charges $55 per hour with no additional fees.
3a.Which mover provides a better deal for two hours of work? How did you arrive at your answer?
MY ANSWER:
Heavy Lifting:
$80(fee)
+$70($35+$35)=2 hours od work
------------------------------
$150 for 2 hours of work
Quick Move:
$110($55+$55)= 2 hours of work
*for two hours of work Quick Move is cheaper by $40.
3b.Which mover provides a better deal for 15 hours of work? How did you arrive at your answer?
MY ANSWER:
Heavy Lifting:
$80(fee)
+$525($35hour x 15 hours=$525)
------------------------------
$605 for 15 hours of work
Quick Move:
$825($55hour x 15 hours=$825)
*for 15 hours of work heavy lifting is cheaper by $220.
3c.This is the question that I really need help with!
For what values h (hours) does Quick move offer the better deal? Express your answer as an inequality. Explain how you reached your answer.
MY ANSWER:
QUICK MOVE offers the better deal for the two hours. I'm hot exactly sure how to put that into an inequality?
2(h)=$110
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! The trick is to find the number of hours where the two companies would charge the same amount. So if the expression for HL is  and the expression for QM is 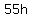 , you need to set these two expressions equal to each other and solve for h:
So now we know that at 4 hours, it doesn't matter which company you choose:
 and  .
From the first two parts of the problem, you know that QM is a better deal at some point less than 4, and HM is a better deal at a point greater than 4.
So your inequality becomes: QM is a better deal if  . Notice that we don't include the 'or equal to' in the inequality because we are looking for QM to be a BETTER deal. If then QM and HL offer the same deal, and the same is not better.
This brings up another point. Could we have said that QM is a better deal if  ? Actually, we can't answer that with the information given, because we don't know whether either company charges a fractional hourly rate for a fraction of an hour used.
If, for example, QM charges $55 for every hour or part of an hour, i.e. 3.5 hours is the same fee as 4 hours, then would be the same as . On the other hand, if they actually charge  for 3.5 hours of use, then the only acceptable answer is .
|
|
|
| |
