|
Question 1207430: A property worth $35 OOO is purchased for 10% down and semi-annual payments of $2100 for 12 years. What is the nominal annual rate of interest if interest is compounded quarterly?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the amount of the loan is equal to .90 * 35000 = 31500.
for a 12 year loan, there are 24 semi-annual payments of 2100, made at the end of each semi-annual time period.
using the ti-business analyst 2 calculator, i get a semi-annual interest rate of 4.160152395%-
divide that by 100 and then add 1 to it to get a semi-annual growth factor of 1.04160152395.
raise that to the second power to get an effective annual growth factor of 1.084933735.
take the fourth root of that to get an effective quarterly growth factor of 1.020588812.
subtract 1 from that and then multiply it by 400 to get a nominal annual growth rate of 8.035524952%.
that should be your answer.
to see if this makes sense, do the following.
assume the nominal interest rate is what you just derived, meaning it is equal to 8.035524952%.
to find the quarterly interest rate, divide that by 4 to get 2.058881238%.
to convert that to a quarterly growth factor, divide it by 100 and then add 1 to it to get 1.02058881238.
raise that to the second power to get an effective semi-annual growth factor of 1.041601524.
subtract 1 from that and then multiply it by 100 to get 4.1601524%.
that's the same semi-annual interest rate that i got using the financial calculator, indicating that the quarterly growth factor is correct.
i'm reasonably sure that this is correct.
your solution should be a nominal annual interest rate of 8.035524952%. which is equal to 8.0355% when rounded to 4 decimal places which is equal to 8.04% when rounded to 2 decimal places.
the financial calculator at can be used to find the semi-annual interest rate.
the result of that analysis is shown below:
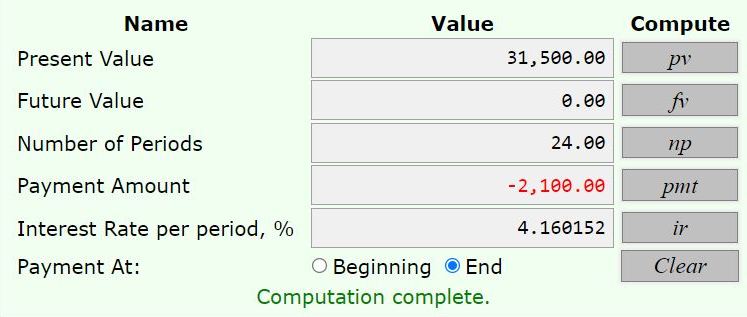
the inputs were:
present value = 31500
future value = 0
number of time periods = 12 years * 2 time periods per year = 24 semi-annual time periods.
the payments at the end of each time period are 2100, shown as -2100 because they are money going out.
click on interest rate % per time period and you get 4.160152%.
this agrees with that i got using the ti-business analyst 2 calculator, when rounding is taken into consideration.
Answer by ikleyn(53421)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A property worth $35,000 is purchased for 10% down and semi-annual payments of $2100 for 12 years.
What is the nominal annual rate of interest if interest is compounded quarterly?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by tutor @Theo has an error (or a typo).
His answer 8.035524952% is incorrect.
I came to bring a correct solution, right numbers and proper answer.
Down payment is 10% of $35,000, i.e. 0.1*35000 = 3500 dollars.
Hence, the loan is the rest amount of $35,000 - $3,500 = $31,500.
+------------------------------------------------------------+
| Notice that, as it is given in the problem, semi-annual |
| payments are desynchronized with quarterly compounding. |
+------------------------------------------------------------+
Nevertheless, we can synchronize payments and compounding by considering an EQUIVALENT scheme
with semi-annual compounding with the effective growth coefficient 'r' semi-annually.
This coefficient 'r' is not known now, and we should find it from the problem.
We then have a loan of $31,500 with semi-annual payments of $2100 and semi-annual compounding
with the effective semi-annual rate of r.
Write the standard loan equation for such a loan
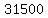 = = 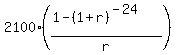
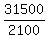 = = 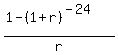 15 =
15 = 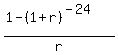 Solve this equation numerically to find 'r'.
I used online calculator https://www.wolframalpha.com/calculators/equation-solver-calculator/
It found the approximate real solution r = 0.0416015.
Thus, in the equivalent scheme, the semi-annual effective rate is 0.0416015.
// Notice that till point my solution coincides with that by @Theo.
Hence, the effective semi-annual growth factor is 1+r = 1.0416015.
It implies that in the basic scheme, the effective quarterly growth factor is the square root of that
Solve this equation numerically to find 'r'.
I used online calculator https://www.wolframalpha.com/calculators/equation-solver-calculator/
It found the approximate real solution r = 0.0416015.
Thus, in the equivalent scheme, the semi-annual effective rate is 0.0416015.
// Notice that till point my solution coincides with that by @Theo.
Hence, the effective semi-annual growth factor is 1+r = 1.0416015.
It implies that in the basic scheme, the effective quarterly growth factor is the square root of that
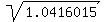 = 1.020589.
Hence, the effective quarterly rate is 0.020589.
Then the annual effective rate is four times this, or 4*0.020589 = 0.082388.
Thus the nominal annual compounding interest is 8.2388%. <<<---=== ANSWER = 1.020589.
Hence, the effective quarterly rate is 0.020589.
Then the annual effective rate is four times this, or 4*0.020589 = 0.082388.
Thus the nominal annual compounding interest is 8.2388%. <<<---=== ANSWER
Solved.
|
|
|
| |