|
Question 1207414: A car was purchased for $1500 down and payments of $265 at the end of each month for four years. Interest is 9% compounded quarterly.
(a) What was the purchase price of the car?
(b) How much interest will be paid?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A car was purchased for $1500 down and payments of $265 at the end of each month for four years.
Interest is 9% compounded quarterly.
(a) What was the purchase price of the car?
(b) How much interest will be paid?
~~~~~~~~~~~~~~~~~~~~~~
The purchase price in this problem is $1500 plus the loaned amount.
About the loan, we know that the payments are $265 at the end of each month
for 4 years at the annual interest rate of 9% compounded quarterly.
It is equivalent to (it works as) quarterly payments of 3*265 = 795 dollars
at the end of each quarter compounded at effective rate r = 0.09/4 per quarter.
Use the formula for periodic payments for the loan at given conditions.
The formula is
Q = 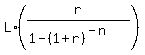 , (1)
where L is the loan amount; r = , (1)
where L is the loan amount; r = 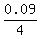 is the effective interest rate per quarter;
n is the number of payments (same as the number of quarters, n = 4*4 = 16);
Q is the quarterly payment of $795.
Substitute these values into the formula and get an equation for quarterly payments
795 = is the effective interest rate per quarter;
n is the number of payments (same as the number of quarters, n = 4*4 = 16);
Q is the quarterly payment of $795.
Substitute these values into the formula and get an equation for quarterly payments
795 = 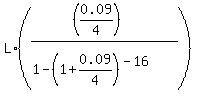 . (2)
We can calculate the coefficient (the factor in the formula) separately . (2)
We can calculate the coefficient (the factor in the formula) separately
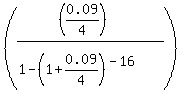 = 0.07511663.
Now from (1) we find L
L = = 0.07511663.
Now from (1) we find L
L = 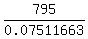 = 10583.54 dollars (rounded to closest cent).
Thus the purchase price for the car was $10583.54 + $1500 = $12083.54.
It is the ANSWER to question (a).
The amount paid back for this loan was 16 payments by 795 dollars = 16*795 = 12720 dollars.
The interest paid for the loan is the difference $12720 - $10583.54 = $2136.46
It is the ANSWER to question (b). = 10583.54 dollars (rounded to closest cent).
Thus the purchase price for the car was $10583.54 + $1500 = $12083.54.
It is the ANSWER to question (a).
The amount paid back for this loan was 16 payments by 795 dollars = 16*795 = 12720 dollars.
The interest paid for the loan is the difference $12720 - $10583.54 = $2136.46
It is the ANSWER to question (b).
Solved.
======================
The solution in the post by @MathLover1 is INCORRECT and IRRELEVANT.
It is enough to point that in her solution she combines monthly payments with quarterly rates,
which is the nonsense out of any elementary logic.
Also, she uses the formula for the future value of an annuity, which is IRRELEVANT,
since in this problem we should use a mathematical model for a loan.
Madam does not know the subject, can not distinct an annuity from a loan,
wrongly uses the annuity formula instead of the loan formula and does not understand
meaning of parameters in her formula.
179% out.
Be aware and ignore her post, for the safety of your mind.
|
|
|
| |