Question 1206609: You deposit $6000 into an account that earns 7% compounded annually. A friend deposits $5500 into an account that earns 6.95% annual interest, compounded continuously. Will your friend's balance ever equal yours? If so, when? If not, enter NEVER.
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
You deposit $6000 into an account that earns 7% compounded annually.
A friend deposits $5500 into an account that earns 6.95% annual interest, compounded continuously.
Will your friend's balance ever equal yours? If so, when? If not, enter NEVER.
~~~~~~~~~~~~~~~~~~~~~~
For your account, the effective annual growth coefficient is 1.07.
For your friend's account, the effective annual growth coefficient is
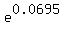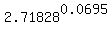 =  = 1.071972011.
As you see, for your friend's account, the effective annual coefficient is greater than your,
so the friend's account is growing faster and will catch with your account somewhen.
To find this catching time moment , write an equation
 =  .
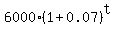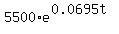It gives
 =  ,
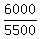1.090909091 =  ,
1.090909091 =  .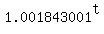
Take logarithm base 10 of both sides
log(1.090909091) = log(1.001843001)*t
and find t
t =  = 47.25528282 years.
Now round 47.25528282 to the closest greater integer year and get the
ANSWER. Your friend's account will be greater than yours in 48 years.
I rounded 47.25528282 to 48 years in order for the bank be able to make the last compounding
with your account to compare the accounts in the same time moment in equal conditions.
Solved.
|
|
|
