Question 1206601: Starting on July 1, 2000, Peter borrows $7000 each year for 4 years from his dear Aunt May to pay for college. (Note: the last date that he borrows money is July 1, 2003.) From the beginning, Aunt May agreed to defer all interest on the loans until Peter finds a job; i.e. Peter's loans will not accumulate any interest until the first day he starts working. After that, Peter will be charged 8.6 percent compounded semiannually, and he will pay Aunt May back with 14 equal semiannual payments, the first coming 6 months after he starts his job. Peter finds a job as a photographer for a local newspaper, and his first day of work is July 1, 2004. For tax reasons, Peter needs to compute the total amount of interest that he will pay to Aunt May in the year 2007. How much in interest did Peter actually pay in 2007?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! by july 1, 2003, he will owe aunt may 28000 dollars.
there is no interest charged until he starts working.
i used the ti-business analyst 2 for determining the payment required at the end of each semi-annual time period.
inputs are:
percent value = 28000
future value = 0
number of time periods = 14 half years.
interest rate per time period = 8.6% / 2 = 4.3% per half year.
payment made at end of each semi-annual time period.
calculator says that the payment at the end of each semi-annual time period = 2703.496789.
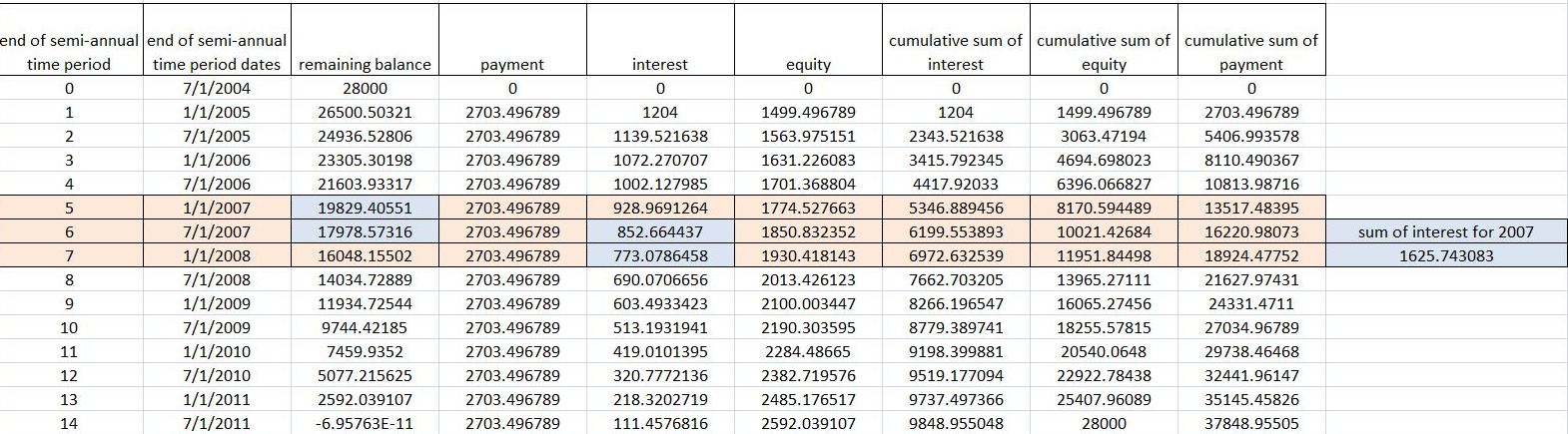
i then used excel to determine the payments and interest and equity charged for each semi-annual time period.
this is what the excel looks like.
the timeline for this problem is as follows:
7/1/2000 first 7000 is borrowed.
7/1/2001 second 7000 is borrowed.
1/1/2002 third 7000 is borrowed.
7/1/2003 fourth 7000 is borrowed.
7/1/2004 first day of work as a photographer.
1/1/2005 first semi-annual payment is made.
1/1/2007 remaining balance of loan at beginning of 2007.
7/1/2007 interest on first payment in 2007.
1/1/2008 interest on last payment in 2007.
the remaining balance on 1/1/2007 = 19829.40551.
the interest charged on this balance is .043 * 19829.40551 = 852.6644369.
the remaining balance on 7/2/2007 = 17978.57316.
the interest charged on this balance is .043 * 17978.57316 = 773.0786458.
the total interest that peter had to pay in the year 2007 is the sum of these two = 1625.743083 = 1625.74 rounded to the nearest penny.
that should be your solution.
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1206601
Starting on July 1, 2000, Peter borrows $7000 each year for 4 years from his dear Aunt May
to pay for college. (Note: the last date that he borrows money is July 1, 2003.)
From the beginning, Aunt May agreed to defer all interest on the loans until Peter finds a job;
i.e. Peter's loans will not accumulate any interest until the first day he starts working.
After that, Peter will be charged 8.6 percent compounded semiannually,
and he will pay Aunt May back with 14 equal semiannual payments,
the first coming 6 months after he starts his job.
Peter finds a job as a photographer for a local newspaper, and his first day of work is July 1, 2004.
For tax reasons, Peter needs to compute the total amount of interest that he will pay to Aunt May
in the year 2007. How much in interest did Peter actually pay in 2007?
~~~~~~~~~~~~~~~~~~~~~~~
Let's make the timeline
July 1, 2000 Peter borrows $7600 The debt becomes $7000,
July 1, 2001 Peter borrows $7600 The debt becomes $14000,
July 1, 2002 Peter borrows $7600 The debt becomes $21000,
July 1, 2003 Peter borrows $7600 The debt becomes $28000,
July 1, 2004 Peter found the job The debt is $28000 and Peter is charged 8.6% compounded semiannually from this date.
So, starting from July 1, 2004 we have classic loan problem:
the loan amount is $30400; it is 8.6% charged semiannually;
the debt should be repayed in 14 equal semiannual payments (two payments per year),
in 7 years (2005, 2006, 2007, 2008, 2009, 20010, 2011).
Make one more timeline
1-st payment Jan 1, 2005 first payment comes 6 months after he starts his job
2-nd payment Jul 1, 2005
3-rd payment Jan 1, 2006
4-th payment Jul 1, 2006
5-th payment Jan 1, 2007
6-th payment Jul 1, 2007
They want you determine the total amount of interest Peter pays in 2007.
So, they want you find the sum of the 5-th and 6-th payments.
Use the Excel function IPMT, which is specially designed to calculate the interest part
of a classic loan scheme for the specific payments.
For description of this function see these sources
wording/text description
https://www.wallstreetprep.com/knowledge/ipmt-function/
Youtube videos
https://www.youtube.com/watch?v=xZq4RNqE7ts
https://www.youtube.com/watch?v=bni0l75lc-8
The format of the function IPMT is as follows
= IPMT(rate, per, nper, principal, fv, type)
In this format, "rate" is the effective rate per period = 0.043 (= 0.086/2 semiannually) required parameter
per = 5 - the payment, of which we want to get the interest part; required parameter
nper = 14 - total number of payments;
principal = 28000; required parameter
fv is optional (we can omit it);
type is optional (we can omit it, which means that
So, we write in Excel cell/spreadsheet for the interest part of the 5-th payment
= IPMT(0.043, 5, 14, 28000), and we get the value of the interest for the 5-th payment of $928.97.
Next, we write in Excel cell/spreadsheet for the interest part of the 6-th payment
= IPMT(0.043, 6, 14, 28000), and we get the value of the interest for the 6-th payment of $852.66.
So, total interest part of the two Peter's payments of the year 2007 is the sum $928.97 + $852.66 = $1,781.63. ANSWER
Solved.
---------------------------
Post-solution notes:
1. My answer is different from that by Theo.
It is because I summed both interest payments for the year 2007 (as the problem requires),
while Theo summed interest payments partly for 2007 and partly for 2008.
2. The solution by @Theo refers to full spreadsheet of all components of payments,
which spreadsheet (is assumed) you should do manually.
(and which you, by the definition, can not do manually, since otherwise you would not post this request).
My solution uses only standard function of Excel, which you can use as just given tool,
which facilitates your job.
In addition, you have full description of the function and the methodology,
so in the future you can easily solve million similar problems easy on your own.
|
|
|