SOLUTION: How much must be placed each month into a retirement account earning 12%compounded month if the value of the account is to rea h $1000000 in 20 years

This problem is to determine the amount of monthly payments/deposits.


Since the payments are at the end of each month, it is a classic Ordinary Annuity saving plan. 
The general formula to start (which is a PREREQUISITE and which you should know from your textbook) is 


    FV = ,    


where  FV is the future value of the account;  P is the monthly payment (deposit); 
r is the monthly effective percentage yield presented as a decimal; 
n is the number of deposits (= the number of years multiplied by 12, in this case).


From this formula, you get for the monthly payment 


    P = .     (1)


Under the given conditions, FV = $1,000,000;  r = 0.12/12 = 0.01;  n = 20*12 = 240.  
So, according to the formula (1), you get for the monthly payment 


    P = 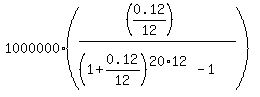 =  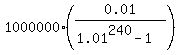= $1010.87.


Answer.  The necessary monthly deposit is $1010.87.