SOLUTION: Please help me with this problem. Would greatly appreciate your help! You win the lottery and get $100 per day for 25 years. Assuming a yearly interest rate of 6%, compounded da

This saving plan of depositing $100 per day for 25 years at a yearly interest rate of 6%, 
compounded daily, is called an ORDINARY ANNUITY plan.


There is a formula to calculate the total amount which the plan generate at the end.


This formula is

    f = ,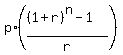


f is the future value
p is the daily payment
r is the interest rate per time period
n is the number of time periods.


In your problem:


time periods are days.
p = 100 dollars  
r = 0.06/365 per day (counting 365 days in a year)
n = 25*365 = 9125 days in 25 years


formula becomes f = 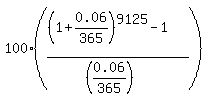 = 2,117,691.45 dollars (rounded).


Now, your problem asks, what amount should be deposited one time today
on the 25 years account giving 6% interest rate annually and compounded daily,
in order for to get the same total of $2,117,691.45 at the end of 25 years?


To determine it, we write this equation for the unknown principal amount P

    2117691.45 = .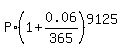


From this equation we get the ANSWER

    P =  = 472579.09.


So, in today's dollars, your winning is EQUIVALENT to  $472,579.09.    ANSWER