|
Question 1201094: You deposit $3000 into an account that earns 7% compounded annually. A friend deposits $2250 into an account that earns 6.85% annual interest, compounded continuously. Will your friend's balance ever equal yours? If so, when? If not, enter NEVER.
They will be equal in about
years (round to nearest whole year)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your two investments are:
3000 * 1.07 ^ x
2250 * e^(.0685 * x)
they will be equal when 3000 * 1.07 ^x = 2250 * e^(.0685*x)
if you graph the difference, they will be equal when 3000 * 1.07^x - 2250 * e^(.0685 *x) = 0
the equivalent annual growth rate to e^(.0685*x) can be found as follows:
e^(.0685) = 1.070900625.
subtract 1 from that to get .070900625.
that's the equivalent annual growth rate.
you get 1.070900625 ^ x = e ^ (.0685 * x)
you can evaluate that for any x and you will see that the results will always be equal.
for example, when x = 40, you get 1.070900625^40 = 15.4869851 and e^(.0685*40) = the same.
you can do that for any x and the resulting values will be the same.
since e^(.0685*x) is equivalent to 1.070900625^x, then you can substitute 1.070900625^x for e^(.0685*x)
since the euivalent annual growth rate is higher than 1.07, it suggests that 3000 * 1.07^x will be equal to 2250 * 1.070900625^x at some point in time.
start with 3000 * 1.07^x = 2250 * 1.070900625^x
divide both sides of that equation by 2250 and divide both sides of that equation by 1.07^x to get:
3000/2250 = 1.070900625^x/1.07^x
take the log of both sides of that eqution to get:
log(3000/2250) = log(1.070900625^x/1.07^x)
by log rule that says log(a/b) = log(a) - log(b), that becomes:
log(3000/2250) = log(1.070900625^x) - log(1.07^x)
by log rule that says log(b^x) = x * log(b), that becomes:
log(3000/2250) = x * log(1.070900625) - x * (log(1.07)
factor out the x to get:
log(3000/2250) = x * (log(1.070900625) - log(1.07)
by log rule that says log(a) - log(b) = log(a/b), that becomes:
log(3000/2250) = x * log(1.070900625/1.07)
divide both sides of the equation by log(1.070900625/1.07) to get:
log(3000/2250) / log(1.070900625/1.07) = x
solve for x to get:
x = 341.9285085
3000 * 1.07^x will be equal to 2025 * 1.070900625 ^ x when x = 341.9285085.
since 1.070900625 ^ x is equivalent to e^(.0685*x), this also says that:
3000 * 1.07^x will be equal to 2025 * e^(.0685*x) when x = 341.9285085.
3000 * 1.07 ^ 341.9285085 = 3.44048223 * 10^13.
2250 * 1.070900625 ^ 341.9285085 = 3.44048223 * 10^13.
2250 * e^(.0685 * 341.9285085) = 3.44048223 * 10^13.
all 3 equations are equal when x = 341.9285085.
your solution is that 3000 * 1.07 ^ x will be equal to 2250 * e^(.0685 * x) in 341.9285085 years.
round to nearest whole year to get 342 years.
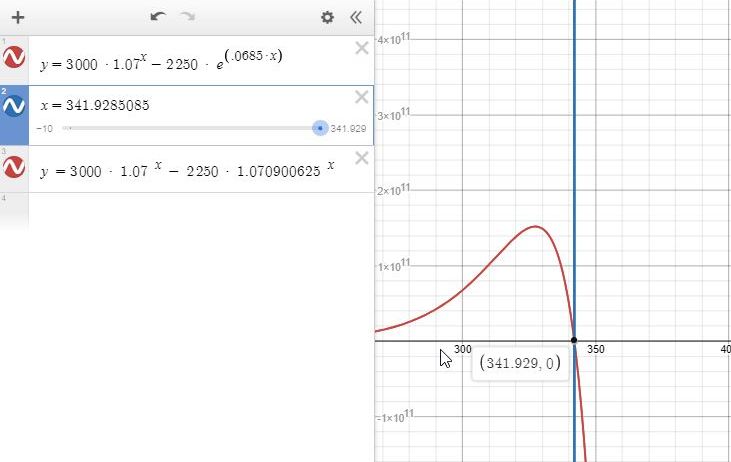
graph y = 3000 * 1.07^x - 2250 * e^(.0685*x) and graph y = 3000 * 1.07^x - 2250 * 1.070900625 ^ x, as shown below.
you will see that the graph crosses y = 0 when x = 341.9285085 for both equations.
here's the graph.
|
|
|
| |