Question 1201069: You invest $ 5000 in Acme Inc. on January 1, 2000. Your investment returns 2.75 % compounded monthly. How much money will you have on June 30, 2006?
Found 4 solutions by mananth, ikleyn, CPhill, MathTherapy:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website!
r = R/100
r = 2.75/100
r = 0.0275 rate per year
Amount A = P(1 + r/n)nt
A = 5,000.00(1 + 0.0275/12)^((12)(6.5))
A = 5,000.00(1 + 0.0023)^(78)
A=$5981
Answer by ikleyn(53618)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You invest $ 5000 in Acme Inc. on January 1, 2000. Your investment returns 2.75 % compounded monthly.
How much money will you have on June 30, 2006?
~~~~~~~~~~~~~~~~~~~~~~~
Calculations and the answer in the post by @mananth are incorrect.
I came to make the job accurately as it should be done.
r = R/100
r = 2.75/100
r = 0.0275 rate per year
Amount A = 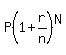 , N is the number of compounding (= the same as the number of months N = 78).
A = , N is the number of compounding (= the same as the number of months N = 78).
A = 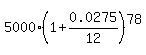 A = $5977.39. ANSWER
A = $5977.39. ANSWER
Solved correctly.
-------------------------
These typical financial problems assume a PRECISE solution correct to one single cent.
It is a standard for banking practice, and it is a standard for solving school/college exercises
in Financial Math, because the answer of an exercise must match to the precise standard value.
To get a precise answer, NEVER make intermediate rounding, since it inevitably leads to loosing precision.
To get a precise answer, use specialized financial calculators, or specialized online calculators,
or Excel spreadsheets.
Answer by CPhill(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! r = R/100
r = 2.75/100
r = 0.0275 rate per year
Amount A = P(1 + r/n)nt
A = 5,000.00(1 + 0.0275/12)^((12)(6.5))
A = 5,000.00(1 + 0.0023)^(78)
A=$5981
Answer by MathTherapy(10719)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You invest $ 5000 in Acme Inc. on January 1, 2000. Your investment returns 2.75 % compounded monthly. How much
money will you have on June 30, 2006?
CAN'T believe those 2 "respondents" rounded too early, as usual, and both came up the same WRONG answr: $5,981.
Is this some kind of mutiny? One AI respondent replicating another's WRONG answer and maybe trying to "drum" up
support for each other's ineptitude?
Formula for the FUTURE VALUE of $1:  , where: , where:
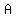 = Accumulated amount/FUTURE VALUE (UNKNOWN, in this case) = Accumulated amount/FUTURE VALUE (UNKNOWN, in this case)
 = Present Value, or Principal invested, or INITIAL amount deposited/Invested ($5,000, in this case) = Present Value, or Principal invested, or INITIAL amount deposited/Invested ($5,000, in this case)
 = Annual Interest rate (2.75%, or .0275, in this case) = Annual Interest rate (2.75%, or .0275, in this case)
 = Number of ANNUAL compounding periods (monthly, or 12, in this case) = Number of ANNUAL compounding periods (monthly, or 12, in this case)
 = Time, in years ( = Time, in years (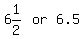 , in this case) , in this case)
 becomes: becomes:  , and then FUTURE VALUE, or , and then FUTURE VALUE, or 
|
|
|