Question 1200996: The Sandersons are planning to refinance their home. The outstanding principal on their original loan is $100,000 and is now to be amortized in 240 equal monthly installments at an interest rate of 5%/year compounded monthly. The new loan they expect to secure is to be amortized over the same period at an interest rate of 4.2%/year compounded monthly. How much less can they expect to pay over the life of the loan in interest payments by refinancing the loan at this time? (Round your answer to the nearest cent.)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! calculator at https://arachnoid.com/finance/
at 5% per year compounded monthly, the payment required is 659.96.
at 4.2% per yer compounded monthly, the payment requred is 616.57.
the difference is 43.39.
payments are made at the end of each month.
240 payments of 659.96 = 158,390.4
the interest is that minus 100,000 = 58,390.4
240 payments of 616.57 = 147,976.8
the interest is tht minus 100,000 = 47,976.8
the difference in the interest payments is 58,390.4 minus 47,976.8 = 10,413.6
that's how much less in interrest is expected to paid after refinancing.
here are the results from the calculator.
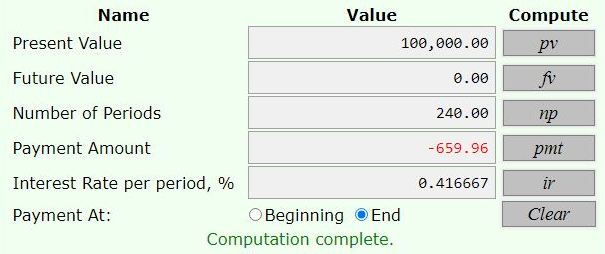
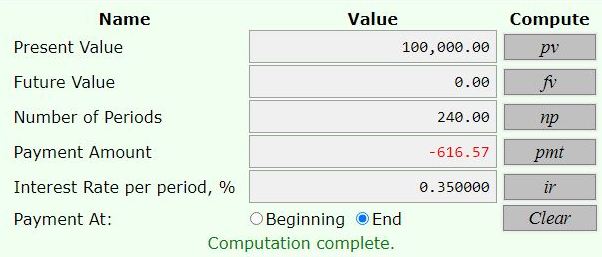
the yearly interest rate is divided by 12 to get the monthly interest rate.
all payments are made at the end of each month.
inputs are everything except payment.
output is payment.
payments are negastive because it's money spent.
|
|
|