Question 1199706: 1) If limt((a/x)*csc((πx/(x - 1)) = 2, (x→ + ∞)
Find the value of a
2) find the set solution of:
iz² - i³|2z²| = 3i×(conj(z))², such z belong complex numbers
Answer by ikleyn(52792)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
2) find the set solution of:
iz² - i³|2z²| = 3i×(conj(z))², such z belong complex numbers
~~~~~~~~~~~~~~~~~~~~~~
In this post, I will solve your second problem, ONLY.
Our starting equation is
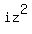 - -  = =  . (1)
Since . (1)
Since  = -1, this equation is the same as = -1, this equation is the same as
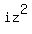 + +  = =  .
We can write it in this equivalent form .
We can write it in this equivalent form
 = =  - - 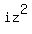 .
We can cancel common factor " i " in both sides .
We can cancel common factor " i " in both sides
 = =  - -  . (2)
Left side is a real number --- hence, right side must be a real number, too.
Ok. Now let z = a+bi. Then from (2), right side of (2) is . (2)
Left side is a real number --- hence, right side must be a real number, too.
Ok. Now let z = a+bi. Then from (2), right side of (2) is
 - - 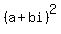 = 3*(a^2 - 2abi - b^2) - (a^2 +2abi - b^2) =
= (3a^2 - 3b^2- a^2 + b^2) + (-6abi - 2abi) = (2a^2 - 2b^2) - 8abi. (3)
Since the right side of (2) is a real number, it implies from (3) that ab = 0, i.e.
EITHER a= 0 OR b= 0 (or BOTH).
So, below we analyze two cases.
(a) b= 0. It means that "z" is, actually, a real number.
It is easy to check, that then equation (2) is valid for any value of real number z,
which means that any real number is the solution for the original equation.
(b) a= 0, b=/= 0. It means that "z" is, actually, a pure imaginary number.
Then in (2), the left side is positive real number, while the right side (3)
is negative real number, which creates a CONTRADICTORY.
+-----------------------------------------------------------------------------+
| So, the = 3*(a^2 - 2abi - b^2) - (a^2 +2abi - b^2) =
= (3a^2 - 3b^2- a^2 + b^2) + (-6abi - 2abi) = (2a^2 - 2b^2) - 8abi. (3)
Since the right side of (2) is a real number, it implies from (3) that ab = 0, i.e.
EITHER a= 0 OR b= 0 (or BOTH).
So, below we analyze two cases.
(a) b= 0. It means that "z" is, actually, a real number.
It is easy to check, that then equation (2) is valid for any value of real number z,
which means that any real number is the solution for the original equation.
(b) a= 0, b=/= 0. It means that "z" is, actually, a pure imaginary number.
Then in (2), the left side is positive real number, while the right side (3)
is negative real number, which creates a CONTRADICTORY.
+-----------------------------------------------------------------------------+
| So, the  to the problem is that |
| the solution set for the given equation is the set of all real numbers. |
+-----------------------------------------------------------------------------+ to the problem is that |
| the solution set for the given equation is the set of all real numbers. |
+-----------------------------------------------------------------------------+
Solved, with full explanations.
|
|
|