Question 1198679: Jane Adele deposits $1,300 in an account at the beginning of each 3-month period for 12 years. If the account pays interest at the rate of 4%, compounded quarterly, how much will she have in her account after 12 years?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jane Adele deposits $1,300 in an account at the beginning of each 3-month period for 12 years.
If the account pays interest at the rate of 4%, compounded quarterly,
how much will she have in her account after 12 years?
~~~~~~~~~~~~~~~~~~~
It is a classic Annuity Due saving plan. The general formula is
FV = 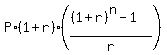 , (1)
where FV is the future value of the account; P is the quarterly payment (deposit)
at the beginning of each payment period; r is the quarterly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 4, in this case).
Under the given conditions, P = 1300; r = 0.04/4 = 0.01; n = 12*4 = 48.
So, according to the formula (1), Jane Adele will get at the end of the 4-th year
FV = , (1)
where FV is the future value of the account; P is the quarterly payment (deposit)
at the beginning of each payment period; r is the quarterly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 4, in this case).
Under the given conditions, P = 1300; r = 0.04/4 = 0.01; n = 12*4 = 48.
So, according to the formula (1), Jane Adele will get at the end of the 4-th year
FV = 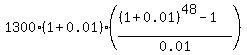 = =  = $80385.28 (rounded).
Note that Jane Adele will deposit only 12*4*$1300 = $62400 in 12 years.
The rest is what the account earns/accumulates in 12 years. = $80385.28 (rounded).
Note that Jane Adele will deposit only 12*4*$1300 = $62400 in 12 years.
The rest is what the account earns/accumulates in 12 years.
-----------------
On Annuity Due saving plans, see the lesson
- Annuity Due saving plans and geometric progressions
in this site.
This lesson contains EVERYTHING you need to know about this subject, in clear and compact form.
|
|
|