Question 1198671: Suppose a state lottery prize of $3 million is to be paid in 25 payments of $120,000 each at the end of each of the next 25 years. If money is worth 11%, compounded annually, what is the present value of the prize? (Round your answer to the nearest cent.)
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose a state lottery prize of $3 million is to be paid in 25 payments of $120,000 each
at the end of each of the next 25 years. If money is worth 11%, compounded annually,
what is the present value of the prize? (Round your answer to the nearest cent.)
~~~~~~~~~~~~~~~~~~~~~~
We have a sinking fund. Its initial value is unknown and we should find it - it is a present value of the fund.
We know that the initial money is deposited for 25 years at 11% annual rate,
paid out $120,000 and compounded (both) at the end of each year.
Use the formula for the present value of such sinking fund
PV = 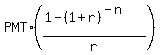 ,
where PV is the present value, PMT is the annual payment value,
r is the annual rate, n is the number of payment/compounding (the number of years, in this problem).
With the given data, the formula for calculations is
PV = ,
where PV is the present value, PMT is the annual payment value,
r is the annual rate, n is the number of payment/compounding (the number of years, in this problem).
With the given data, the formula for calculations is
PV = 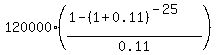 = = 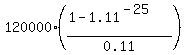 = 1,010,609.36 dollars.
ANSWER. The present value of the prize is $1,010,609.36.
This amount should be deposited initially, and it will provide
no-failure payments of $120,000 at the end of each year during 25 years,
under given conditions. = 1,010,609.36 dollars.
ANSWER. The present value of the prize is $1,010,609.36.
This amount should be deposited initially, and it will provide
no-failure payments of $120,000 at the end of each year during 25 years,
under given conditions.
Solved.
|
|
|