Question 1198670: Mr. Gordon plans to invest $300 at the end of each month in an account that pays 6%, compounded monthly. After how many months will the account be worth $30,000?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Mr. Gordon plans to invest $300 at the end of each month in an account that pays 6%,
compounded monthly. After how many months will the account be worth $30,000?
~~~~~~~~~~~~~~
The formula for an Ordinary Annuity saving account compounded monthly is
FV = 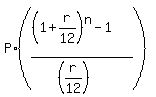 where FV is the future value, P is the monthly payment at the end of each month,
r is the interest rate per year expressed as a decimal,
n is the number of monthly deposits (the number of months).
So, we need to find " n " from this equation
where FV is the future value, P is the monthly payment at the end of each month,
r is the interest rate per year expressed as a decimal,
n is the number of monthly deposits (the number of months).
So, we need to find " n " from this equation
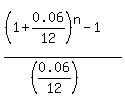 = = 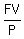 = = 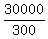 = 100,
Thus the equation is = 100,
Thus the equation is
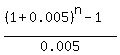 = 100.
Rewrite it in this form = 100.
Rewrite it in this form
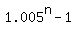 = 0.005*100, = 0.005*100,
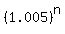 = 1 + 0.005*100 = 1.5.
Take the logarithm base 10 of both sides
n*log(1.005) = log(1.5)
and calculate
n = = 1 + 0.005*100 = 1.5.
Take the logarithm base 10 of both sides
n*log(1.005) = log(1.5)
and calculate
n = 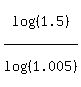 = 81.296 months.
We should round it to the closest greater integer, which is 82 months,
in order for the bank be in position to make the last compounding.
ANSWER. 82 months.
CHECK. = 81.296 months.
We should round it to the closest greater integer, which is 82 months,
in order for the bank be in position to make the last compounding.
ANSWER. 82 months.
CHECK. 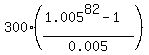 = 30316.75, which is greater than 30000; = 30316.75, which is greater than 30000;
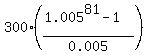 = 29867.41, which is less than 30000. = 29867.41, which is less than 30000.
Solved, checked, explained and completed.
-----------------------
On ordinary annuity saving plan, see my lessons in this site
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
|
|
|