|
Question 1190654: What is the present value of an ordinary annuity having semi-annual payments of 8,000 pesos for 12 years with an interest rate of 12% compounded annually?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to calculate the present value of the ordinary annuity:
**1. Determine the effective interest rate per payment period:**
Since payments are semi-annual, but the interest is compounded annually we need to find the effective semi-annual rate. We can't simply divide the annual rate by two, instead we find the equivalent rate such that if we compound the semi-annual rate twice we get the annual rate. The formula to convert is:
(1 + annual rate) = (1 + semi-annual rate)^2
(1 + 0.12) = (1 + semi-annual rate)^2
1.12 = (1 + semi-annual rate)^2
sqrt(1.12) = 1 + semi-annual rate
1.0583 = 1 + semi-annual rate
semi-annual rate = 1.0583 - 1
semi-annual rate = 0.0583 or 5.83%
**2. Determine the number of payment periods:**
* The annuity lasts for 12 years.
* Payments are made semi-annually, meaning twice a year.
* Number of payment periods (n) = 12 years * 2 payments/year = 24 periods
**3. Use the present value of an ordinary annuity formula:**
PV = PMT * [1 - (1 + r)^-n] / r
Where:
* PV = Present Value (what we want to find)
* PMT = Payment amount per period (8,000 pesos)
* r = Interest rate per period (0.0583 or 5.83% as a decimal)
* n = Number of periods (24)
**4. Calculate:**
PV = 8000 * [1 - (1 + 0.0583)^-24] / 0.0583
PV = 8000 * [1 - (1.0583)^-24] / 0.0583
PV = 8000 * [1 - 0.2452] / 0.0583
PV = 8000 * 0.7548 / 0.0583
PV = 8000 * 12.9468
PV ≈ 103,574.27 pesos
Therefore, the present value of the ordinary annuity is approximately 103,574.27 pesos.
Answer by ikleyn(52747)  (Show Source):
You can put this solution on YOUR website! .
What is the present value of an ordinary annuity having semi-annual payments of 8,000 pesos
for 12 years with an interest rate of 12% compounded annually?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is INCORRECT.
Indeed, @CPhill introduces " equivalent " scheme with semi-annual compounding,
but in this problem, the bank makes compounding annually - it DOES NOT make compounding semi-annually.
So, the way, which @CPhill treats and solves for this problem is INADEQUATE.
To solve this problem, we should consider annual compounding with annual payments of 2*8000 = 16000 pesos.
Then the formula for the present value is
PV = 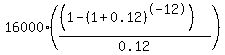 = 99109.99 pesos. ANSWER
In this problem, deposits of 8000 pesos, made at the middle of each year, lie in the bank without movement
and wait for the end of the year.
At the end of the year, this money is combined with the deposit made at the end of the year,
and only then the two combined deposits are the subject for compounding.
Solved correctly.
|
|
|
| |
