|
Question 1190209: The manager of the Sweet Candy Shop wishes to mix candy worth $4 per pound, $6 per pound, and $10 per pound to get 100 pounds of a mixture worth $7.60 per pound. The amount of $10 candy must equal the total amounts of the $4 and the $6 candy. How many pounds of each must be used?
Found 3 solutions by ikleyn, josgarithmetic, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
The manager of the Sweet Candy Shop wishes to mix candy worth $4 per pound, $6 per pound, and $10 per pound
to get 100 pounds of a mixture worth $7.60 per pound. The amount of $10 candy must equal the total amounts
of the $4 and the $6 candy. How many pounds of each must be used?
~~~~~~~~~~~~~~~~~
As you read the condition, you understand that the amount of the $10 candy is exactly half of the total 100 pounds,
i.e. exactly 50 pounds, as well as the combined amount of the $4 and $6 candies is exactly the other half
of 100 pounds, i.e. 50 pounds.
So, regarding $10 candies, you just know the answer: it is 50 pounds.
To solve for the rest candies, let's assume that the anount of the $6 candies is x pounds;
then the amount of the $4 candies is (50-x) pounds.
Then the cost of the mixture is 6x + 4*(50-x) + 50*10 dollars.
We want it would be 7.60*100 dollars. So, we write the total cost equation
6x + 4*(50-x) + 50*10 = 7.60*100.
Simplify and find x
6x + 200 - 4x + 500 = 760
6x - 4x = 760 - 500 - 200.
2x = 60
x = 60/2 = 30.
ANSWER. Use 30 pounds of the $6 candy; 50-30 = 20 pounds of the $4 candy and 50 pounds of the $10 candy.
CHECK. The average cost is 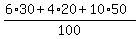 = 7.60 dollars per pound. ! Precisely correct !
Solved.
Answer by josgarithmetic(39617)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The amount of $10 candy is equal to the total amounts of the $4 and $6 candy; and the total amount of candy is 100 pounds. Therefore, there are 50 pounds of the $10 candy.
The 50 pounds of the $10 candy are worth $500; the total 100 pounds of the mixture at $7.60 per pound is worth $760. So the value of the combined $4 and $6 candy is $260.
50 pounds of $4 coffee would be worth $200; 50 pounds of $6 coffee would be worth $300; the actual value of the $4 and $6 candy together is $260.
Look at the three values $200, $260, and $300 on a number line and observe/calculate that 260 is 60/100 = 3/5 of the way from 200 to 300. That means 3/5 of the 50 pounds of $4 and $6 candy must be the $6 candy.
So there is 3/5 of 50 pounds, or 30 pounds, of $6 candy and 20 pounds of $4 candy.
ANSWER: 50 pounds of $10 candy, 30 pounds of $6 candy, and 20 pounds of $4 candy
CHECK:
50(10)+30(6)+20(4) = 500+180+80 = 760
100(7.60) = 760
|
|
|
| |
