|
Question 1189865: A certain brand of house paint must be purchased either in quarts at $12 each or in gallons at $18 each. A painter needs a 3-gallon mixture of the paint consisting of 3 parts blue and 2 parts white. What is the least amount of money needed to purchase sufficient quantities of the two colors to make the mixture?
a)$54 b)$60 c)$66 d)$90 e)$144
Found 2 solutions by ikleyn, ankor@dixie-net.com:
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A certain brand of house paint must be purchased either in quarts at $12 each or in gallons at $18 each.
A painter needs a 3-gallon mixture of the paint consisting of 3 parts blue and 2 parts white.
What is the least amount of money needed to purchase sufficient quantities of the two colors
to make the mixture?
a)$54 b)$60 c)$66 d)$90 e)$144
~~~~~~~~~~~~~~
This problem is to apply common sense and a bit of arithmetic and simple algebra.
To start, notice that
1 gallon = 4 quarts, and
buying in gallons is much cheaper than buying the same amount in quarts, both for blue and for white paint.
The parts of the 3-gallon mixture are 1.8 gallons of blue paint and 1.2 gallons of white paint
(easy calculate with algebra 3x + 2x = 3 gallons; 5x = 3 gallons; x = 0.6 of a gallon; and the parts are 3x and 2x).
+---------------------------------------------------------------------------------+
| So, we can solve the problem (minimize the cost) separately |
| for 1.8 gallons of the blue paint and for 1.2 gallons of the white paint. |
+---------------------------------------------------------------------------------+
1.8 gallons of the blue paint is the same as 1 gallon and 3.2 quarts,
so for 1.8 gallons of the blue paint we have two options:
to buy 1 gallon plus 4 quarts separately, which costs 18 + 4*12 = 66 dollars,
or to buy 2 gallons (which is enough), which costs 2*18 = 36 dollars.
The choice is clear, and we buy 2 gallons of the blue paint, paying 36 dollars.
1.2 gallons of the white paint is the same as 1 gallon and 0.8 quarts,
so for 1.2 gallons of the white paint we have two options:
to buy 1 gallon plus 1 quarts, which costs 18 + 12 = 30 dollars,
or to buy 2 gallons (which is enough), which costs 2*18 = 36 dollars.
The choice is clear, and we buy 1 gallon plus 1 quart of the white paint, paying 30 dollars.
In total, the optimal purchase costs 36 + 30 = 66 dollars. ANSWER
Solved.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A certain brand of house paint must be purchased either in quarts at $12 each or in gallons at $18 each.
A painter needs a 3-gallon mixture of the paint consisting of 3 parts blue and 2 parts white.
What is the least amount of money needed to purchase sufficient quantities of the two colors to make the mixture?
:
3 gal = 12 qts
let b = amt of blue paint in quarts
let w = amt of white
:
b + w = 12
and using the ratio of blue to white
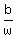 = = 
2b = 3w
b = (3w)/2
b = 1.5w
find in terms of w
1.5w + w = 12
2.5w = 12
w = 12/2.5
w = 4.8 quarts of white required
then
b = 12 - 4.8 = 7.2 quarts of blue
subtract no. of whole gallons from each, cost 2 *18 = $36
.8qts of white and 3.2 qts of blue close enough to 4, get another gal of blue
that would now be 3 * 18 = $54 plus 1 qt of white, 54 + 12 = $66
:
Summarize $66: 2 gal of blue ($36), 1 gal and 1 qt of white, ($18 + $12)
|
|
|
| |