Question 1185474: Akshi has five exams scores of 66,64,84,58,and 79. In her Latin class. What score does she need on the final exam to have a mean grade of 70? Round your answer to two decimal places,if necessary. ( ALL exams have a maximum of 100 points.)
Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39618)   (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
To have an average of 70 on 6 tests, the total of her scores needs to be 6*70=420.
Add the given five test scores and subtract that total from 420 to get the answer.
Or you can do it like this, by comparing each of the five given test scores to the desired average:
66 -4
64 -6
84 +14
58 -12
79 +9
--------
-22+23 = +1
Overall, her current five test scores put her 1 point above her desired average; that means her next score must be 1 point below that average.
ANSWER: She needs a score of 69 (-1) on her next test to get an average of 70.
Answer by ikleyn(52795)  (Show Source):
You can put this solution on YOUR website! .
Akshi has five exams scores of 66,64,84,58,and 79. In her Latin class. What score does she need on the final exam
to have a mean grade of 70? Round your answer to two decimal places,if necessary. ( ALL exams have a maximum of 100 points.)
~~~~~~~~~~~~~~~~
Let the unknown score at the 6-th exam be x.
Then you have this equation for x, which expresses the average 70 of the six exams
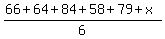 = 70.
Multiply both sides by 6 and simplify
x = 70*6 - 66 - 64 - 84 - 58 - 79 = 69.
ANSWER. The minimum score she needs on the final exam to get average 70 is 69.
Solved.
--------------
Note that @josgarithmetic has an error in his setup equation (just fixed after my note).
@greenestamps has an error in his calculations (just fixed after my note).
//////////////
To see many other similar (and different) solved problems, look into the lessons
- Solved problems on average scores, weight, height and temperature
- Solved problems on average scores
- Solved problems on average age
- Miscellaneous problems on average values
in this site.
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
|
|
|
