|
Question 1179080: Grandma decides to put 1300 dollars every month into an account for you. She makes 23 monthly deposits, the last coming September 1, 2003 - the day you start college. She wants you to be able to withdraw money from this account at the beginning of each month, with the first withdrawal coming September 1, 2003 and the last coming June 1, 2008, (when you'll graduate). (Note: that makes 58 withdrawals total.) How much will you be able to withdraw each month if the account is earning a nominal interest rate of 9.3 percent convertible monthly?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break this problem into two parts:
**Part 1: Calculate the Accumulated Value of Grandma's Deposits**
1. **Monthly Deposit:** $1300
2. **Number of Deposits:** 23
3. **Interest Rate:** 9.3% convertible monthly (0.093 / 12 = 0.00775 per month)
We'll use the future value of an ordinary annuity formula:
FV = P * [((1 + r)^n - 1) / r]
Where:
* FV = Future Value
* P = Periodic Payment ($1300)
* r = Interest Rate per Period (0.00775)
* n = Number of Periods (23)
FV = 1300 * [((1 + 0.00775)^23 - 1) / 0.00775]
FV = 1300 * [(1.00775^23 - 1) / 0.00775]
FV = 1300 * [(1.196398246 - 1) / 0.00775]
FV = 1300 * [0.196398246 / 0.00775]
FV = 1300 * 25.3416
FV ≈ $32944.08
**Part 2: Calculate the Monthly Withdrawal Amount**
1. **Accumulated Value (Present Value for Withdrawals):** $32944.08
2. **Number of Withdrawals:** 58
3. **Interest Rate:** 9.3% convertible monthly (0.093 / 12 = 0.00775 per month)
We'll use the present value of an annuity due formula since withdrawals are at the beginning of each month:
PV = M * [(1 - (1 + r)^-n) / r] * (1 + r)
Where:
* PV = Present Value ($32944.08)
* M = Monthly Withdrawal Amount
* r = Interest Rate per Period (0.00775)
* n = Number of Periods (58)
Rearrange the formula to solve for M:
M = PV / [((1 - (1 + r)^-n) / r) * (1 + r)]
M = 32944.08 / [((1 - (1.00775)^-58) / 0.00775) * (1.00775)]
M = 32944.08 / [((1 - 0.62791485) / 0.00775) * 1.00775]
M = 32944.08 / [(0.37208515 / 0.00775) * 1.00775]
M = 32944.08 / [48.010987 * 1.00775]
M = 32944.08 / 48.382093
M ≈ $681.09
**Answer:**
You will be able to withdraw approximately $681.09 each month.
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Grandma decides to put 1300 dollars every month into an account for you. She makes 23 monthly deposits,
the last coming September 1, 2003 - the day you start college. She wants you to be able to withdraw money
from this account at the beginning of each month, with the first withdrawal coming September 1, 2003
and the last coming June 1, 2008, (when you'll graduate). (Note: that makes 58 withdrawals total.)
How much will you be able to withdraw each month if the account is earning a nominal interest rate
of 9.3 percent convertible monthly?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem uses the term " convertible " instead of " compounded ".
This term " convertible " is NEVER USED in this context.
I performed all calculations accurately in a way as it SHOULD be done.
My numbers and my answer are different from that by @CPhill.
Let's break this problem into two parts:
**Part 1: Calculate the Accumulated Value of Grandma's Deposits**
1. **Monthly Deposit:** $1300
2. **Number of Deposits:** 23
3. **Interest Rate:** 9.3% compounded monthly (effective rate r = 0.093/12 per month)
We'll use the future value of an ordinary annuity formula:
FV = 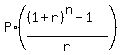 , (1)
where
* FV = Future Value
* P = Periodic Payment ($1300)
* r = Interest Rate per Period (0.00775)
* n = Number of Periods (23)
FV = , (1)
where
* FV = Future Value
* P = Periodic Payment ($1300)
* r = Interest Rate per Period (0.00775)
* n = Number of Periods (23)
FV = 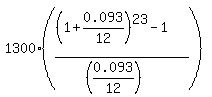 (2)
I used MS Excel software in my computer.
It is commonly considered as an appropriate tool for such calculations,
since it provides the necessary precision.
I copied and pasted this formula into a MS Excel, and I got the value of $32,592.78.
I did not make intermediate rounding, since intermediate rounding are PROHIBITED
in such calculation: they influence to the final result and lead to wrong answer.
I checked this value using an online calculator at this web-site
https://www.omnicalculator.com/finance/annuity-future-value
https://www.omnicalculator.com/finance/annuity-future-value
I got precisely the same dollars and precisely the same cents.
**Part 2: Calculate the Monthly Withdrawal Amount**
1. **Accumulated Value (Present Value for Withdrawals):** $32592.78
2. **Number of Withdrawals:** 58
3. **Interest Rate:** 9.3% monthly (effective compounding rate r = 0.093/12 per month)
We'll use the present value of an annuity due formula since withdrawals are at the beginning of each month:
PV = (2)
I used MS Excel software in my computer.
It is commonly considered as an appropriate tool for such calculations,
since it provides the necessary precision.
I copied and pasted this formula into a MS Excel, and I got the value of $32,592.78.
I did not make intermediate rounding, since intermediate rounding are PROHIBITED
in such calculation: they influence to the final result and lead to wrong answer.
I checked this value using an online calculator at this web-site
https://www.omnicalculator.com/finance/annuity-future-value
https://www.omnicalculator.com/finance/annuity-future-value
I got precisely the same dollars and precisely the same cents.
**Part 2: Calculate the Monthly Withdrawal Amount**
1. **Accumulated Value (Present Value for Withdrawals):** $32592.78
2. **Number of Withdrawals:** 58
3. **Interest Rate:** 9.3% monthly (effective compounding rate r = 0.093/12 per month)
We'll use the present value of an annuity due formula since withdrawals are at the beginning of each month:
PV = 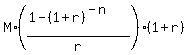 , (3)
where:
* PV = Present Value ($32592.78)
* M = Monthly Withdrawal Amount
* r = Interest Rate per Period (0.093/12)
* n = Number of Periods (58)
Rearrange the formula (3) to solve for M:
M = , (3)
where:
* PV = Present Value ($32592.78)
* M = Monthly Withdrawal Amount
* r = Interest Rate per Period (0.093/12)
* n = Number of Periods (58)
Rearrange the formula (3) to solve for M:
M = 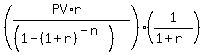 , (4)
M = , (4)
M = 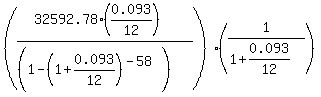 . (5)
Again, I used MS Excel software in my computer.
It is commonly considered as an appropriate tool for such calculations,
since it provides the necessary precision.
I copied and pasted this formula into a MS Excel, and I got the value of $694.43.
I did not make intermediate rounding, since intermediate rounding are PROHIBITED
in such calculation: they influence to the final result and lead to wrong answer.
Answer. You will be able to withdraw approximately $694.43 at the beginning of each month. . (5)
Again, I used MS Excel software in my computer.
It is commonly considered as an appropriate tool for such calculations,
since it provides the necessary precision.
I copied and pasted this formula into a MS Excel, and I got the value of $694.43.
I did not make intermediate rounding, since intermediate rounding are PROHIBITED
in such calculation: they influence to the final result and lead to wrong answer.
Answer. You will be able to withdraw approximately $694.43 at the beginning of each month.
Solved.
===================================
Dear @CPhill,
I want you do understand me correctly.
After all, in real life it does not matter, if you make a mistake in 10 cents or even in one dollar.
But if you are an " Artificial Intelligence ", you have no right to make a computational mistake even in one cent.
You either use a commonly accepted, trusted, proven computing methodology,
or, as an alternative, NOBODY and NEVER will trust you.
|
|
|
| |