SOLUTION: A carpenter purchased 70 ft of redwood and 80 ft of pine for a total cost of $335. A second purchase, at the same prices, included 100 ft of redwood and 50 ft of pine for a total c

Let x = price per 1 ft of redwood;  y = price for 1 ft of pine.


Then you have the system of these 2 equations in 2 unknowns


    70x + 80y = 335    (1)

   100x + 50y = 395    (2)


Appliy any method you want (you know, you like). I will use the determinant method (= same as the Cramer's rule)


    x = 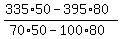 = 3.30 dollars per foot

    y =  = 1.30 dollars per foot.

Let cost of each foot of redwood and pine, be R and P, respectively

We then get: 70R + 80P = 335______14R + 16P = 67 ------- eq (i)

100R + 50P = 395_____20R + 10P = 79 ------- eq (ii)

6R - 6P = 12 ------ Subtracting eq (i) from eq (ii)

6(R - P) = 6(2)______R - P = 2________R = 2 + P ------- eq (iii) 



14(2 + P) + 16P = 67 ------- Substituting 2 + P for R in eq (i)

28 + 14P + 16P = 67

30P = 39

Cost of each foot of pine, or 

R = 2 + 1.30 ------- Substituting 1.30 for P in eq (iii)

Cost of each foot of redwood: