|
Question 1168648: A person invests $4050 in stocks today, and their value doubles every 4 years. Let f (t) be the value (in dollars) of the investment at t years from now
A. Find an equation of f.
B Find the value of the investment 20 years from now
a. f can be modeled by the exponential equation of the form f(t)=ab^t with the following values kof a and b.
THE ANSWERS I NEED TO FIND ARE:
a=
b=
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you are given that the investment doubles every 4 years.
since your investment period is 20 years, then 4 goes into 20 five times.
your future value will be 4050*2^5 = 129,600.
if you want to model this using continuous compounding formula, you would do the following.
the continuous compounding formula is f = p*e^(r*t)
f is the future value and p is the present value and r is the interest rate per time period and t is the number of time periods.
to use this formula, consider p = 4050 and f = 129600 amd t = 20 years.
the formula becomes 129600 = 4050*e^(r*20)
divide both sides of this formula by 4050 to get:
129600/4050 = e^(r*20)
take the natural log of both sides of this formula to get:
ln(129600/4050) = ln(e^(r*20))
since ln(e^(r*20)) is equal to r*20*ln(e), the formula becomes:
ln(129600/4050) = r*20*ln(e)
since ln(e) = 1, the formula becomes:
ln(129600/4050) = r*20
divide both sides of this formula by 20 to get:
ln(129600/4050)/20 = r
solve for r to get:
r = .1732867951.
to confirm, replace r in the formula with that to get:
129600 = 4050 * e ^ (.1732867951*20) becomes 129600 = 129600.
this confirms the value of r is correct.
with discrete compounding, the formula used is f = p*(1+r)^n
f is the future value, p is the present value, r is the interest rate per time period, n is the number of time periods.
assuming the investment doubles every 4 years, and assuming that the money is compounding annually, you would do the following:
when the money doubles every 4 years, f = 2, p = 1, r = what you want to find, n = 4
the formula becomes 2 = 1*(1+r)^4
simplify to get 2 = (1+r)^4
take the 4th root of both sides of this equation to get:
(2)^(1/4)=1+r
subtract 1 from both sides of this equation to get:
(2)^(1/4)-1 = r
solve for r to get:
r = .189207115.
that's the interest rate per year.
the discrete compounding formula becomes f = 4050*(1+.189207115)^20
f is the future value
p is the present value
r = .189207115 per year.
n = 20 years.
solve for f to get f = 129600.
you can graph all three of these equations to get the same answer.
here's the graph.
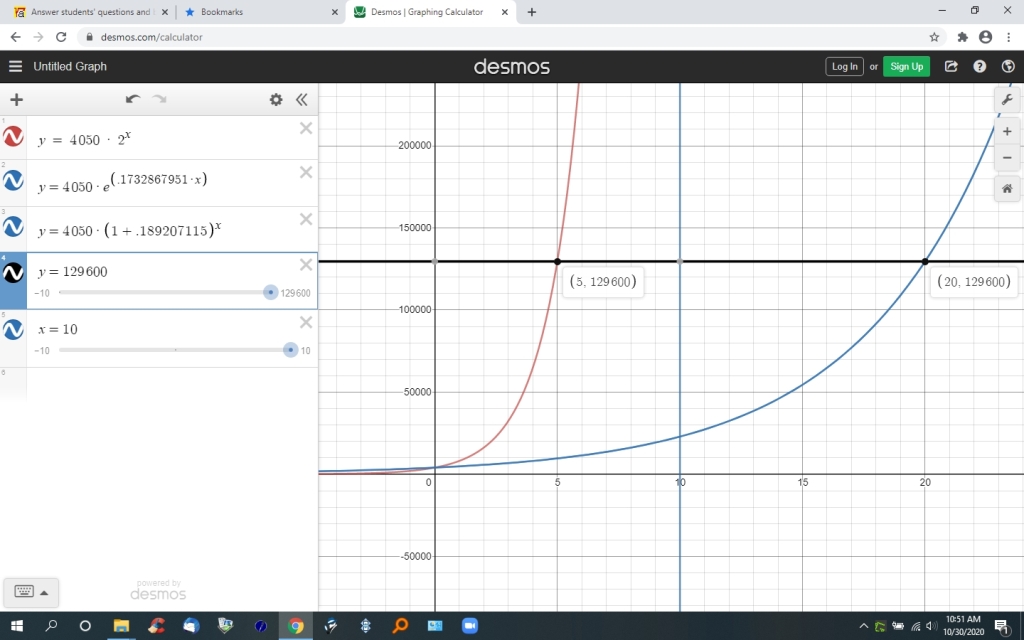
the red graph has each interval of x representing 4 years.
therefore, 20 years is when x = 5.
the blue graph has each interval of x representing 1 year.
therefore, 20 years is when x = 20.
the blue graph represents both the discrete compounding formula and the continuous compounding formula.
since these two formulas are equivalent to each other, the same blue graph represents both.
any questions about any of this, let me know and i'll answer as best and as soon as i can.
theo
Answer by ikleyn(52944)   (Show Source): (Show Source):
|
|
|
| |