|
Question 1168455: Having some trouble with this one. Any help is appreciated
Suppose Miss Roxanne Davenport is 25 years old right now and puts away $1,800 per quarter in an account that returns 6% interest.
a. How much will be in the account when she turns 65?
b. What is her total contribution to the account?
c. How much interest did she earn?
Found 3 solutions by Theo, MathTherapy, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you would handle this in the following fashion.
first you need the right formula or a financial calculator.
we'll do the formula and then i'll show you how to do it with an online calculator and then i'll show you how to do it using cash NPV and cash flow through excel.
any one of these will do the job, with various amounts of effort and expertise on our part.
fyi, the manual calculations come from the following tutorial that you might be interested in.
https://www.algebra.com/algebra/homework/Finance/THEO-2016-04-29.lesson#f3
so does the reference to the online financial calculators.
normally, the payment is made at the end of each time period, so the formula you need is:
FUTURE VALUE OF AN ANNUITY WITH END OF TIME PERIOD PAYMENTS
f = (a*((1+r)^n-1))/r
f is the future value of the annuity.
a is the annuity.
r is the interest rate per time period.
n is the number of time periods
in your problem, the money is being invested at the end of each quarter and the money is assumed to be compounded each quarter as well.
you are investing at the end of each quarter, so a = 1400
the interest rate if 6% per year compounded quarterly, so r = 6% divided by 4 to get 1.5% per quarter and then divided by 100 to get .015 per quarter.
that's because the formula uses rate and not percent.
she's 25 now and will take the money out of the account when she's 65. unless told otherwise, the underlying assumption is that these are whole years and not partial years.
65 minus 25 = 40 years * 4 quarters per year = 160 quarters, so n = 160.
you have:
a = 1400
r = .015
n = 160
your formula of f = (a*((1+r)^n-1))/r becomes:
f = (1400*((1+.005)^160-1))/.005
solve for f to get f = 917,323.08
that's how much will be in the account when she turns 65.
her total contribution to the account is 160 * 1400 = 224,000.
the total interest that she earned = 917,323.08 minus 224,000 = 693,323.08.
if you used the financial calculator provided in the tutorial, you would do the following.
pv = 0
fv = 0
np = 160
pmt = -1400
ir = 1.5
payment made at the end of each time period.
you would then click on fv and the calculator will tell you that fv = 917,323.08.
this can be seen below.

the following excel printout shows you the remaining balance in each quarter and the payment in each quarter and the interest earned in each quarter for the first few time period and the last few time periods.
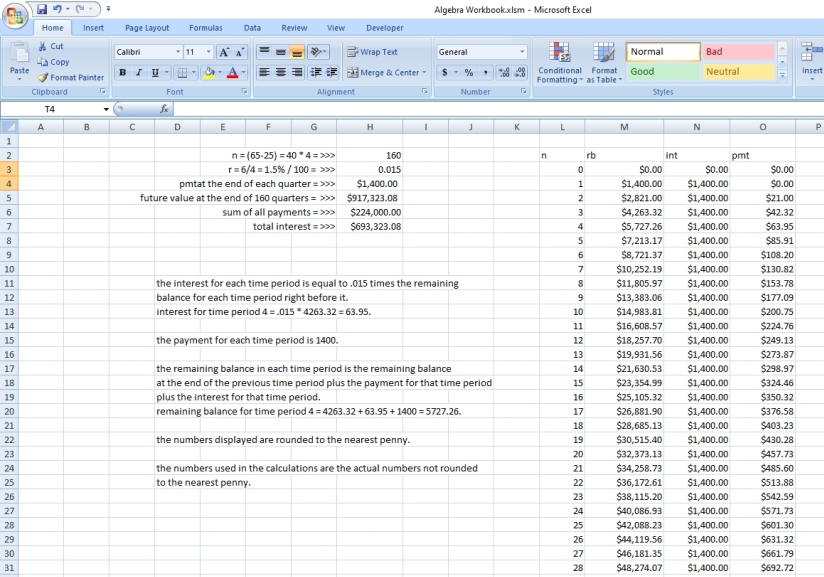
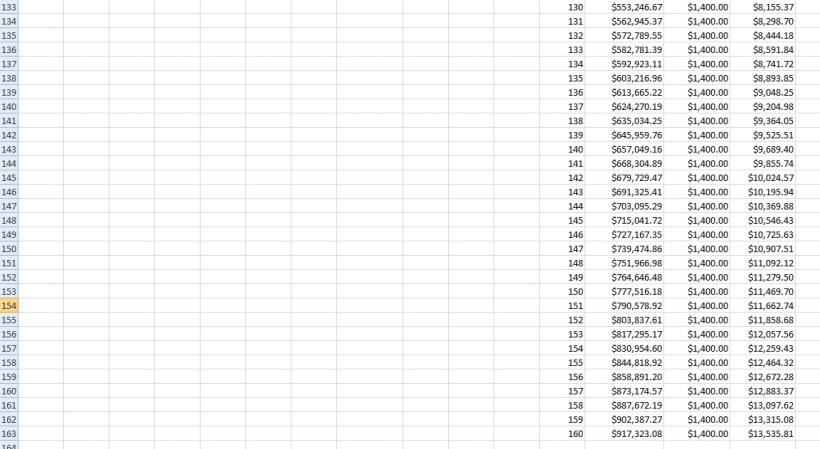
the financial calculator used can be found at https://arachnoid.com/finance/index.html
any further questions, give me a shout.
theo
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is a classic Ordinary Annuity saving plan. The general formula is
FV =  , (1)
where FV is the future value of the account; P is the quarterly payment (deposit); r is the quarterly percentage
yield presented as a decimal; n is the number of deposits (= the number of years multiplied by 4, in this case 4*40 = 160).
Under the given conditions, P = 1800; r = 0.06/4; n = 4*40 = 160. So, according to the formula (1),
she will get at the end of the 40-th year
FV = , (1)
where FV is the future value of the account; P is the quarterly payment (deposit); r is the quarterly percentage
yield presented as a decimal; n is the number of deposits (= the number of years multiplied by 4, in this case 4*40 = 160).
Under the given conditions, P = 1800; r = 0.06/4; n = 4*40 = 160. So, according to the formula (1),
she will get at the end of the 40-th year
FV = 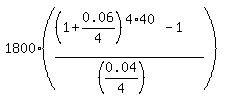 = = 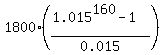 = $1,179,415.39.
Note that she deposits only 4*40*$1800 = $288,000. The rest
1,179,415.39 - 288,000 = 891,415.39 dollars
is the interest that the account earns/accumulates in 40 years. = $1,179,415.39.
Note that she deposits only 4*40*$1800 = $288,000. The rest
1,179,415.39 - 288,000 = 891,415.39 dollars
is the interest that the account earns/accumulates in 40 years.
-----------------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
|
|
|
| |