Question 1167807: A vehicle purchase for $25,000 depreciates at a constant rate of 8% determine the approximate value of the vehicle 14 years after purchase round to the nearest whole dollar
Found 2 solutions by Boreal, Theo:
Answer by Boreal(15235)   (Show Source):
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! the vehicle is purchased for 25,000 dollars.
it loses 8% of value each year.
the formula to use is f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the rate of growth each year
n is the number of years.
the rate of growth per year is equal to the percent growth each year / 100.
therefore, a percent growth of -8% each year equals a rate of growth each year of -.08.
when p = 25,000 and r = -.08 and n = 14, the formula becomes:
f = 25,000 * (1 - .08) ^ 14 = 7779.820763.
the value of the car after 14 years is 7780 dollars.
this can be seen on a graph.
let y = the value of the car.
the equation is y = 25000 * (1 - .08) ^ x = 25000 * .92 ^ x
this is what the graph looks like.
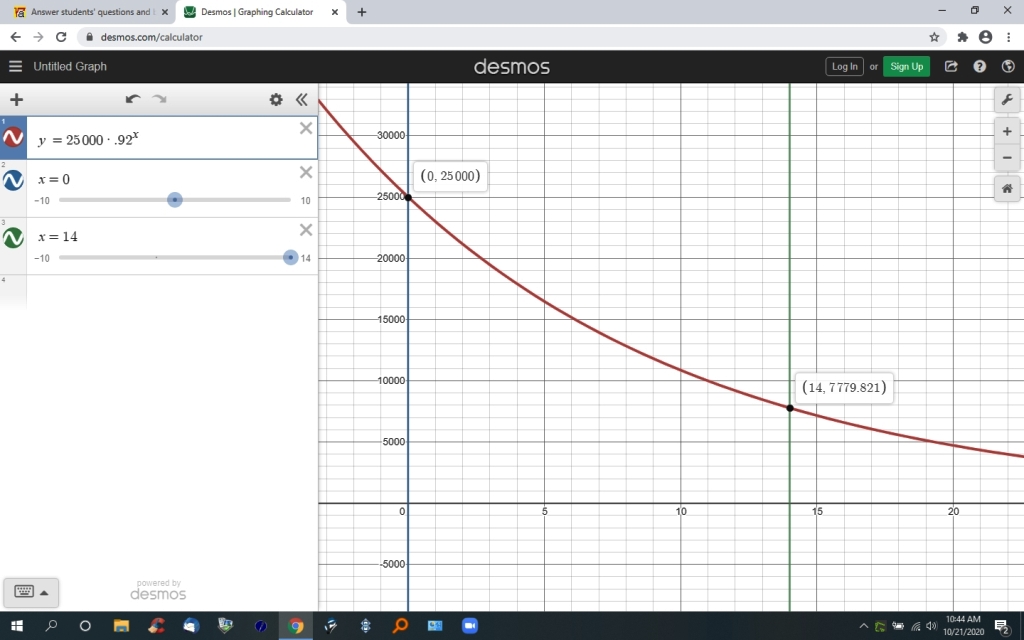
the coordinate points on the graph are in (x,y) format.
x is the number of years.
y is the value of the car.
on the graph, when x = 14, y = 7779.821.
round y to the nearest integer to get y = 7780.
|
|
|
